Produit sinus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 24 Nov 2006, 23:27
par sue » 24 Nov 2006, 23:27
salut,
je me permet de déplacer le sujet ici si qqn aurait une idée pour me débloquer :
je cherche à déduir que
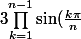= \frac{n}{2^{n-1}})
.
à partir de:
)

----
voilà ce que j'ai fait jusqu'à mnt mais j'en suis pas sure :
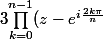 = e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1} (1-e^{i\frac{2(k-1)\pi}{n}}) =e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1} -2i sin(\frac{\pi(k-1)}{n}) = 2^{n-1}e^{i\frac{2\pi}{n}} \prod_{k=0}^{n-1}- i sin(\frac{\pi(k-1)}{n}) = ...)
merci !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 00:42
par aviateurpilot » 25 Nov 2006, 00:42
on pose
=z^n-1=\bigprod_{k=0}^{n-1}(z-e^{2k\pi/n}))
et
=1+z+z^2+...+z^{n-1})
on a
=(z-1)Q(z))
donc
=0\ car\ 1-e^{2k\pi/n}\neq 0)
par suite
=\bigprod_{k=1}^{n-1}(z-e^{2k\pi/n}))
on remplace

par

=n)
et
=|Q(1)|=\bigprod_{k=1}^{n-1}|e^{k\pi/n}|.|e^{-k\pi/n}-e^{+k\pi/n}|=2^{n-1}|i^{n-1}|.\bigprod_{k=1}^{n-1}sin(k\pi/n).|e^{k\pi/n}|=2^{n-1}\bigprod_{k=1}^{n-1}sin(k\pi/n))
donc
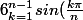=\frac{n}{2^{n-1}})
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 25 Nov 2006, 02:47
par sue » 25 Nov 2006, 02:47
ah merci bcp aviateurpilot c'est bien détaillé j'ai tout compris :++:
au fait j'y ai pas du tout pensé !
merci encore :we:
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Nov 2006, 04:14
par Nicolas_75 » 25 Nov 2006, 04:14
Bonjour,
Je suis très surpris. N'est-ce pas plutôt
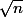
au numérateur du membre de droite ?
EDIT : j'ai dit une bêtise, pardon.
Confusion avec :

-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Nov 2006, 04:49
par Nicolas_75 » 25 Nov 2006, 04:49
Je n'ai rien dit. Pardon. Oubliez mon message.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 11:25
par aviateurpilot » 25 Nov 2006, 11:25
sue a écrit: merci bcp aviateurpilot
de rien
suepour 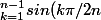)
on a
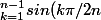=\bigprod_{k=1}^{n-1}cos((n-k)\pi/2n)=\bigprod_{k=1}^{n-1}cos(k\pi/2n))
donc
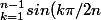\)^2=\bigprod_{k=1}^{n-1}sin(k\pi/2n)cos(k\pi/n)=\bigprod_{k=1}^{n-1}\frac{sin(k\pi/n)}{2}=\frac{1}{2^{n-1}}\bigprod_{k=1}^{n-1}sin(k\pi/n)=\frac{n}{2^{2(n-1)}})
c/c:
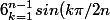=\frac{\sqrt{n}}{2^{n-1}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités