Produit de séries entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
par rifly01 » 12 Déc 2007, 12:25
Bonjour,
J'ai à multiplier quelques séries et j'ai quelques questions qui me viennent :
- Est-ce qu'on peut multiplier des séries ayant des rayons différents ?
Moi j'ai supposé que oui.
Voici un exemple :
)
On sait que
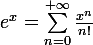
et
=\sum_{n=0}^{+\infty}\frac{(-1)^n x^{n+1}}{n+1})
avec
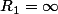
et
On fait le produit des deux séries entières :
=\left(\sum_{n=0}^{+\infty}\frac{x^n}{n!}\right) \times \left(\sum_{n=0}^{+\infty}\frac{(-1)^n x^{n+1}}{n+1}\right)=\sum_{n=0}^{+\infty}\left( \sum_{k=0}^{n}\frac{1}{k!}\frac{(-1)^{n-k}}{n-k+1}\right)x^n)
avec
)
Est-ce que c'est bon ?
Merci d'avance,
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 12 Déc 2007, 13:38
Bonjour,
d'accord pour
mais il n'y a pas un problème d'indice ? Pour la première série le terme général est
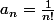
et pour la deuxième
^{n-1}}{n})
et
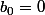
, non ?
-
rifly01
- Membre Relatif
- Messages: 460
- Enregistré le: 30 Déc 2005, 04:38
-
par rifly01 » 12 Déc 2007, 21:39
Ah, oui :
Je reprends :
=x\times \left(\sum_{n=0}^{+\infty}\frac{x^n}{n!}\right) \times \left(\sum_{n=0}^{+\infty}\frac{(-1)^n x^{n}}{n+1}\right)=x\times \sum_{n=0}^{+\infty}\left( \sum_{k=0}^{n}\frac{1}{k!}\frac{(-1)^{n-k}}{n-k+1}\right)x^n)
avec
J'espère que c'est bon maintenant.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
