Bonjour je bloque à un exercice et j'aurais besoin d'un coup de pouce, voici l'énoncé :
Soit n appartenant à N, n\geq 2. On se place dans E = Matrices carrées d'ordre n dans R. On pose I=In.
\varphi : ExE -> R
(A,B) -> <A|B> = tr(tAB)
Je ne sais pas comment bien le faire mais : <A|B> (A scalaire B) = trace(transposée(A)xB), j’espère que c'est clair...
1) J'ai dû montrer que c'était un produit scalaire sur E, sans problème et j'ai dû calculer <M|I> et j'ai trouvé que cela valait la tr(M).
2) On désigne par J la matrice de E dont tous les coefficients sont égaux à 1. On pose F=Vect(I,J).
a) Calculer J² en fonction de J. En déduire <J|J>. J'ai trouvé que J² = nJ et donc que <J|J> = n²
Voilà ou je coince :
b) On note Pf(M) le projeté orthogonal sur F d'une matrice M de E. En remarquant que <M|J> = <Pf(M)|J>, exprimer Pf(M) comme combinaison linéaire de I et J en fonction de tr(M) et du réel \mu = <M|J>.
Je n'ai aucune idée de comment faire... Quelqu'un sait ?
Et enfin la derniere question est :
c) Calculer \mu en fonction des coefficients de M
Merci d'avance
Produit scalaire sur un espace vectoriel
6 messages
- Page 1 sur 1
Re: Produit scalaire sur un espace vectoriel
Pose a priori = \alpha I+\beta J) , et ensuite tire les conséquences du fait que
, et ensuite tire les conséquences du fait que \mid J\rangle = \langle M\mid J\rangle) et
et \mid I\rangle = \langle M\mid I\rangle) (tu as déjà calculé
(tu as déjà calculé  ,
,  et
et  ).
).
Re: Produit scalaire sur un espace vectoriel
J'ai essayé mais je n'y arrive vraiment pas... As tu un autre conseil ?
Re: Produit scalaire sur un espace vectoriel
Un autre conseil ? Oui : persévérer !
 tu sais quoi.
tu sais quoi.
 , c'est l'énoncé qui pose ça.
, c'est l'énoncé qui pose ça.
\mid I\rangle = \langle \alpha I+\beta J\mid I\rangle={?})
\mid J\rangle = \langle \alpha I+\beta J\mid J\rangle={?})
Rappel :) est caractérisé par 1°)
est caractérisé par 1°) \in F) et 2°
et 2° \mid A\rangle =\langle M\mid A\rangle) pour tout
pour tout  .
.
Rappel :
Re: Produit scalaire sur un espace vectoriel
<Pf(M)|A> \neq <M|A>. Enfin on ne sait pas parce qu'on dit juste que cette égalité est vraie avec J qui est une matrice remplie de 1.
Sinon je trouve que :
<Pf(M)|J> = \alpha n + \beta n²
<Pf(M)|I> = \alpha n + \beta n
Mais je ne vois pas où cela mène... Système ?
Sinon je trouve que :
<Pf(M)|J> = \alpha n + \beta n²
<Pf(M)|I> = \alpha n + \beta n
Mais je ne vois pas où cela mène... Système ?
Re: Produit scalaire sur un espace vectoriel
Tu devrais revoir tes notions sur la projection orthogonale.
Par définition de la projection orthogonale sur le sous-espace
sur le sous-espace 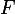 ,
, -M) est orthogonal à
est orthogonal à 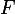 . D'accord ? Je te laisse vérifier que ça veut bien dire que pour tout
. D'accord ? Je te laisse vérifier que ça veut bien dire que pour tout  ,
, \mid A\rangle =\langle M\mid A\rangle) .
.
Enfin, à quoi cela mène ? À répondre à la question posée, qui est, je te le rappelle : "exprimer) comme combinaison linéaire de
comme combinaison linéaire de 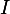 et
et  en fonction de
en fonction de ) et du réel
et du réel 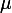 ". Autrement dit, déterminer
". Autrement dit, déterminer 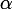 et
et 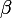 .
.
Par définition de la projection orthogonale
Enfin, à quoi cela mène ? À répondre à la question posée, qui est, je te le rappelle : "exprimer
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
