Produit scalaire euclidien

[Diaz]

Bonjour à tous!

Je vous remercie pour l'aide considérable que vous m'avez apportée jusqu'ici:je me sens de plus en plus prêt,pour ce fameux concours qui me donne des insomnies.
En traitant une ancienne épreuve,j'ai rencontré cet exercice qui m'a posé problème:
Appelons R l'ensemble des réels et R(n) le produit de R, n fois(i.e R(n)=RxRx...xR,n fois).
Soient A un ouvert convexe non vide de R(n) et f une fonction numérique différentiable définie sur A.
Montrer que si f est convexe,alors:
Pour tous a et x appartenant à A,(f(x)-f(a)) >=;
">="signifie "supérieur ou égal à"
On note <.,.> le produit scalaire euclidien dans R(n) et on rappelle qu'une fonction est convexe si et seulement si elle vérifie:pour tous a et s appartenant à A,pour tout t appartenant au segment [0,1],f(tx+(1-t)a)<=tf(x)+(1-t)f(a)
N.B:Si je n'ai pas pu résoudre ce problème,c'est parce que je ne connais pas la définition de produit scalaire euclidien dans R(n):Quelqu'un peut-il me la donner,S.V.P?
D'autre part,j'aimerais quand même que vous m'aidiez à résoudre ce problème.
MERCI!

[abcd22]

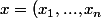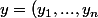Le produit scalaire euclidien (canonique) de deux vecteurs et est .

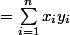
PS : Tu devrais acheter un livre si tu n'as pas de cours sur les espaces préhilbertiens, euclidiens, hermitiens... Tu aurais un plan construit avec les liens entre les objets et les démonstrations :happy3:

[Diaz]

Merci pour le conseil,mais j'ai déjà un livre là-dessus;je ne pose pas mes questions par défaut de documentation,mais plutôt par souci de compréhension.
Pour revenir au produit scalaire euclidien,je me doutais bien que c'était cela la définition;mais,à présent,mon problème est de savoir comment appliquer cela à df(a),qui n'est pas un vecteur de R(n),mais plutôt une application linéaire.
Merci!

[abcd22]

En fait je pense qu'ici df(a) désigne le gradient de f en a (qui est donc bien un vecteur de R(n)), et donc = df(a)(x-a) (sauf que df(a) ne désigne pas la même chose des deux côtés de l'égalité).
En dimension 1 l'inégalité traduit le fait que f est au-dessus de ses tangentes (car elle est convexe), en dimension n c'est une généralisation mais j'ai pas cherché la démonstration, je pense qu'on peut y arriver en se ramenant à une fonction d'une variable g(t) = f(tx + (1-t)a) (on étudie f sur le segment [x,a], avec a et x fixés), si tu montres que g est convexe, en utlisant sa tangente en t=0 on a le résultat.