Produit Scalaire et développement

[jeulstein]

Bonjour,
j'ai un concours a passer avec au programme :
produit scalaire et développement limité
Est-ce que quelqu'un pourrait m'expliquer clairement rapidement comment ça marche !
Merci

[mathelot]

faire un développement limité d'une fonction f au voisignage de zéro
c'est calculer une valeur approchée de f(x) à l'aide d'une expression
polynomiale.
Par exemple,
donne une valeur approchée facilement calculable du réel pour x petit.
On peut écrire une définition plus précise:
la fonction f admet un développement limité à l'ordre n au voisinage de zéro
s'il existe un intervalle ]-h;+h[, (n+1) réels
et une fonction tels que:

avec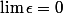 qd x tend vers zéro.
est le reste du développement limité.
f admet un développement limité à l'ordre n au voisinage de a si la fonction
g définie par g(h)=f(a+h) admet un développement limité à l'ordre n au voisinage de zéro. f s'écrit alors:

et la fonction tend vers zéro qd x tend vers a.
Il y a un théorème important:
celui de Taylor-Young:
si f est de classe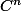 au voisinage de a et que existe, alors f admet un développement limité à l'ordre n+1 au voisinage de a et son développement s'écrit:

Une autre formule de Taylor, dite "avec reste intégral" donne le reste du développement limité sous la forme d'une intégrale.
Noter que l'on peut calculer des développements limités en dérivant et en intégrant terme à terme au vosinage de a dans le cas restreint où f admet
des dérivées de tous ordre en x=a et si elle est somme de sa série de Taylor
dans un voisinage de a.

[Gnörf]

Noter que l'on peut calculer des développements limités en dérivant ...

Attention, il n'est possible de deriver que si l'on sait que f' possède un developpement limité d'ordre n-1 au voisinage d'un point a
Ainsi admet un developpement limité d'ordre 2 au voisinage de 0 ( ), est dériveable sur IR mais f' n'admet pas de developpement limité d'ordre 1 ...