Produit de puissances

[abc]

Bonjour,
J'ai observé les égalités suivantes:
2^1 * (2^4 -1) = 30 (nombre de 2 chiffres)
2^2 * (2^20 -1) = 4 194 300 (nombre de 7 chiffres)
2^3 * (2^100 -1) = 10...3 000 (nombre de 32 chiffres)
2^4 * (2^500 -1) = 52...30 000 (nombre de 152 chiffres)
2^5 * (2^2500 -1) = 12...300 000 (nombre de 755 chiffres)
2^6 * (2^12500 -1) = 479...3 000 000 (nombre de 3 765 chiffres)
2^7 * (2^62500 -1) = 3 033...30 000 000 (nombre de 18 817 chiffres)

À chaque itération un zéro s'ajoute à la fin. Est-ce que cela continue indéfiniment comme je le pense?
Comment le démontrer?
Merci de me venir en aide!

[GaBuZoMeu]

Tu demandes si, pour tout entier naturel ,



où n'est pas divisible par . En divisant par 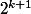ceci revient à



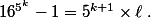
Puisque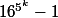 est impair, ne peut pas être divisible par . Finalement, il suffit de vérifier que 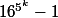est divisible par 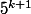pour tout entier naturel . Ça se fait sans grande difficulté par récurrence, je te laisse finir le travail.

[abc]

Merci bien. Je vais essayer cela!

[abc]

On vérifie effectivement que 16^(5^k)-1 est divisible par 5^(k+1) si k=1 ou si k=2. On suppose que 16^(5^k)-1 est divisible par 5^(k+1) mais faudrait démontrer la divisibilité dans le cas où on remplace k par k+1, mais je n'arrive pas à démontrer que 16^(5^(k+1))-1 est divisible par 5^(k+2).

[abc]

Merci encore GaBuZoMeu pour ton aide.
J'ai réussi la démonstration par récurrence.

[GaBuZoMeu]

, à appliquer au bon pour le pas de récurrence.

[abc]

Merci GaBuZoMeu!

[GaBuZoMeu]

Avec plaisir