Produit de deux ensembles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Aoû 2014, 13:52
par barbu23 » 10 Aoû 2014, 13:52
Bonjour à tous,
Soit
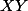
un produit de deux ensembles quelconques

et

.
Soient

une partie de

et

une partie de

.
Comment exprimer
^{ \mathrm{c} } $)
, le complémentaire de
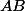
, en foncton de
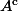
( complémentaire de

) et
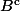
( complémentaire de

) ?.
Voici ce que je fait moi :
 \in X \times Y $)
:
 \in \Big( A \times B \Big)^{ \mathrm{c} } \ \ \Longleftrightarrow \ \ (x,y) \not \in A \times B \ \ \Longleftrightarrow \ \ (x,y) \in A^{\mathrm{c}} \times Y \ \mathrm{ou} \ (x,y) \in X \times B^{\mathrm{c}} \ \ \Longleftrightarrow \ \ (x,y) \in \Big( A^{\mathrm{c}} \times Y \Big) \bigcup \Big( X \times B^{\mathrm{c}} \ \Big) \ \ $)
 \in ??? \ $)
Quelqu'un peut -il me dire par quoi remplacer :
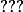
?
Merci d'avance.
-
Nicolas.L
- Membre Naturel
- Messages: 79
- Enregistré le: 07 Aoû 2014, 15:34
-
 par Nicolas.L » 10 Aoû 2014, 21:03
par Nicolas.L » 10 Aoû 2014, 21:03
J'ai peur de dire une bêtise car je n'ai jamais réfléchi à ça avant mais j'ai l'impression qu'il est impossible de simplifier d'aller plus loin que ta dernière expression.
Pour exprimer non(A et B) en fonction de non A et non B on est obligé de dire (Non A) ou (Non B), et si l'on suppose que (x,y) est dans X*Y,
 \in \left( A \times B \right) ^c)
est la négation de " x est dans A et y est dans B "
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 11 Aoû 2014, 00:46
par mrif » 11 Aoû 2014, 00:46
barbu23 a écrit:Bonjour à tous,
Soit
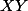
un produit de deux ensembles quelconques

et

.
Soient

une partie de

et

une partie de

.
Comment exprimer
^{ \mathrm{c} } $)
, le complémentaire de
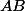
, en foncton de
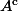
( complémentaire de

) et
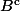
( complémentaire de

) ?.
Voici ce que je fait moi :
 \in X \times Y $)
:
 \in \Big( A \times B \Big)^{ \mathrm{c} } \ \ \Longleftrightarrow \ \ (x,y) \not \in A \times B \ \ \Longleftrightarrow \ \ (x,y) \in A^{\mathrm{c}} \times Y \ \mathrm{ou} \ (x,y) \in X \times B^{\mathrm{c}} \ \ \Longleftrightarrow \ \ (x,y) \in \Big( A^{\mathrm{c}} \times Y \Big) \bigcup \Big( X \times B^{\mathrm{c}} \ \Big) \ \ $)
 \in ??? \ $)
Quelqu'un peut -il me dire par quoi remplacer :
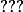
?
Merci d'avance.
Dans ton dernier résultat, tu remplaces
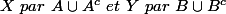
-
soradia1
- Membre Naturel
- Messages: 54
- Enregistré le: 08 Sep 2013, 21:51
-
 par soradia1 » 11 Aoû 2014, 03:26
par soradia1 » 11 Aoû 2014, 03:26
Bonjour, si tu veux une expression sans X et Y, la voici:
^c = (A^c \times B)\cup (A \times B^c)\cup (A^c \times B^c))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
un produit de deux ensembles quelconques
et
.
une partie de
et
une partie de
.
, le complémentaire de
, en foncton de
( complémentaire de
) et
( complémentaire de
) ?.
:
?