Produit de convolution [4ème semestre de license]

[Apeiron]

Bonjour ^^

Petite question d'analyse, si vous le voulez bien.
Je travaille sur les bases du produit de convolution : (f*g)(x) = int(de+oo à -oo)[f(y)g(x-y)dy].

Dans cet exercice, f et g sont définies continues et à support compact.
(définition : F est à support compact s'il existe R>0 tel que |x|>R => f(x)=0 )

Il s'agit de montrer que :
1) f*g est bien définie, continue sur IR et à support compact
2) Si en plus g est de classe C^k, alors f*g est de classe C*k

Commençons par le 1) (ce qui parait raisonnable ^^)

Comme f et g sont à support compact, alors il existe R,R'>0 tels que :
|x|>R => f(x)=0 d'une part, et d'autre part |x|>R' => g(x)=0
Comme R et R' sont des réels, alors ou R<=R' ou R'<=R.
Dans le premier cas, int(de+oo à -oo)[f(y)g(x-y)dy] = int(de+R à -R)[f(y)g(x-y)dy] < +oo
Dans le second cas, int(de+oo à -oo)[f(y)g(x-y)dy] = int(de+R' à -R')[g(y)f(x-y)dy] < +oo (le produit de convolution est commutatif).
Est-ce suffisant pour dire que f*g est bien défini sur IR ou faut-il une autre propriété?

Ensuite, dire que f et g sont continues suffit-il pour dire que f*g est continu, ou faut-il une autre propriété ?

Ensuite, pour montrer que f*g est à support compact, je pense qu'il faut jouer avec des inégalités dans l'intégrale, mais je n'ai pas encore trouvé le cosh. Une idée ?

On verra le 2) après ^^

Merci d'avance.

[Apeiron]

Pour le 2) je me demandais si on ne pouvais par faire une intégration par partie, ou se servir d'une propriété.

Mais personne ne veut m'aider ?

[busard_des_roseaux]

bjr,

Il faut faire les choses "à la main".

La fonction
a les mêmes propriétés que g:
si g est à support compact, aussi. Si g est de classe Ck,
de même.
En suite, une translation de x, pour x fixé ne change rien.

l'application
est la composée des applications:
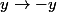(difféomorphisme )
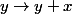(translation = difféomorphisme )

d'où:

a les mêmes propriétés que g.

ensuite, il suffit d'appliquer les théorèmes de continuité et dérivabilité
sous le signe somme et de dériver k fois sous le signe somme le
facteur k fois dérivable.


On doit utiliser trois propriétés:
- la mesure de lebesgue est invariante par translation
- la somme K1+K2 de deux compacts d'un e.v est compacte.
(en effet y appartient à un support compact et pour la dérivation
par rapport à x, propriété locale, on peut restreindre x à un voisinage
compact de .)
- la convolution x-y peut s'écrire soit sur f, soit sur g,
comme on le voit par changement de variable z=x-y
ce qui permet de vérifier la classe Ck par rapport à la variable x
avec le facteur f (par exemple si f est de classe Ck et pas g)


désolé de ne pouvoir t'aider davantage, à part ces quelques idées.

[Apeiron]

Merci.

C'est bon.