Produit de complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 30 Déc 2013, 18:08
par eludante » 30 Déc 2013, 18:08
Bonjour,
Pour faire cours, voici l'énoncé :Calculer
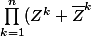)
(en fonction de

et

) avec

Donc calculer :
(Z^2+\overline Z^2)...(Z^n+\overline Z^n)) Mon avancement :
Mon avancement :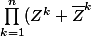=\prod_{k=1}^{n}\rho^k (e^{ik\theta}+e^{-ik\theta})=2^n\rho^{\frac{n(n+1)}{2}}\prod_{k=1}^{n}cos(k\theta))
Sachant que
=\frac {e^{ix}+e^{-ix}}{2})
J'aimerais de l'aide pour calculer ce produit de cosinus ou sinon une autre piste pourrait surement m'aider.
Merci
-
Frede
- Membre Naturel
- Messages: 55
- Enregistré le: 27 Déc 2013, 11:47
-
 par Frede » 30 Déc 2013, 20:04
par Frede » 30 Déc 2013, 20:04
Je réponds rapidement pour le cas où il y aurait urgence. Je pense que tu t'es engagée sur une impasse. Les complexes sont traîtres, je pense que (Zk+Z barre k) doit pouvoir se mettre sous la forme d'un produit commençant par (Z+Z barre) ou peut-être (Z + i*Z barre). Mais c'est juste une idée au pif.
J'y réfléchis et je reviens demain
-
Frede
- Membre Naturel
- Messages: 55
- Enregistré le: 27 Déc 2013, 11:47
-
 par Frede » 31 Déc 2013, 09:16
par Frede » 31 Déc 2013, 09:16
La nuit porte conseil. Je pensais à la formule a²+b²=(a+ib)(a-ib) mais après réflexion, je pense qu'elle ne peut rien nous apporter.
J'abandonne la piste sur laquelle tu t'étais lancée car je sais que quand on a un problème de trigo dont on arrive pas à se sortir, l'astuce c'est de le transformer en problème sur les complexes. Je ne pense pas qu'il serait malin de faire le contraire ici.
Es-tu censée savoir que (cos theta + i sin theta) = e puissance (i theta) ?
Si oui, je pense que c'est de ça qu'il faut partir ici.
Je suis nouveau dans ce groupe et je n'arrive pas à écrire les puissances de la façon normale, c'est pourquoi j'écris comme dans une réponse simple et j'abrège un peu.
En faisant abstraction des rho, tu auras
(Z^n) + (Z barre^n) = (e^i n theta)+(e^ -i n theta)
soit en posant E:=e^i theta
=E + 1/E soit (E² + 1)/E
Le terme suivant sera E² + 1/E² soit (E^4 + 1)/E²
Le terme suivant sera E³ + 1/E³ soit (E^6 + 1)/E³
Le produit des dénominateurs sera facile à effectuer. En ce qui concerne le produit des numérateurs, je te laisse réfléchir.
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 01 Jan 2014, 16:06
par eludante » 01 Jan 2014, 16:06
Donc avec ta méthode je trouve :
}{2}})
Soit avec ta notation :
\times (E^4+1)\times ... \times (E^{2n}+1)}{E^{\frac{n(n+1)}{2}})
Effectivement le produit du dénominateur n'est pas très dur mais je ne vois pas trop comment faire celui du numérateur... Je vais continuer à chercher, en tout cas je te remercie de m'avoir donné une piste !
Edit: ça à l'air d'être une suite géométrique mais je n'en suis pas certain...
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 01 Jan 2014, 18:44
par eludante » 01 Jan 2014, 18:44
Bon et bien je ne trouve toujours pas... Quelqu'un peut m'aider avec ce problème ? J'ai beau essayer tout ce que je connais mais rien n'y fait, je ne trouve pas la solution :(
-
Frede
- Membre Naturel
- Messages: 55
- Enregistré le: 27 Déc 2013, 11:47
-
 par Frede » 01 Jan 2014, 19:49
par Frede » 01 Jan 2014, 19:49
Si je développe le numérateur j'obtiens
avec les deux premiers termes:

ce qui est plutôt sympa.
avec le terme suivant:

Ce serait très bien s'il n'y avait pas un

en trop.
avec le terme suivant:



Soit en ordonnant:


ce qui redevient sympa
car la 1ère ligne vaut
/ (E^2 -1))
et la deuxième me parait simplifiable aussi.
Il faudrait pouvoir dire ce que ça donne avec n facteurs. J'y réfléchis...
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 01 Jan 2014, 23:20
par Rha » 01 Jan 2014, 23:20
Bonsoir,
Si vous voulez une autre piste, vous pouvez étudier la fonction qui au réel

associe
 = \prod \limits_{k=1}^n \cos(kx))
.
En dérivant, on voit que

est solution de
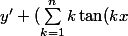)y = 0)
sur

.
edit: Suis-je bête, on retombe sur le produit de départ!
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 02 Jan 2014, 18:30
par eludante » 02 Jan 2014, 18:30
J'ai toujours rien trouvé... Si quelqu'un peut me donner un petit coup de pouce ce serais bien sympa
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 12:43
par eludante » 03 Jan 2014, 12:43
J'ai toujours rien trouvé... Si quelqu'un peut me donner un petit coup de pouce ce serais bien sympa
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 15:25
par eludante » 03 Jan 2014, 15:25
Effectivement je me suis trompé mais ça ne résous toujours pas le problème :(.
Merci quand même
-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 18:06
par eludante » 03 Jan 2014, 18:06
Je suis en 1er année prépa MPSI et je n'ai pas encore vu les coefficients de Tchebychev. Je pense que la solution est bien plus simple. D'ailleurs le résultat ne doit pas comporté de somme (

) ni de produit (
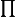
) mais seulement des fonctions de

et

-
eludante
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2013, 17:19
-
 par eludante » 03 Jan 2014, 19:25
par eludante » 03 Jan 2014, 19:25
Qu'est-ce que j'ai dis de mal ? Je ne fais absolument aucune critique, c'est pas la peine de réagir comme ça.
-
Frede
- Membre Naturel
- Messages: 55
- Enregistré le: 27 Déc 2013, 11:47
-
 par Frede » 03 Jan 2014, 19:37
par Frede » 03 Jan 2014, 19:37
Salut, c'est l'emmerdeur qui revient avec sa piste effrayante que personne n'a eu envie d'étudier et pourtant, je crois bien que c'était la bonne piste et que je tiens la réponse.
Mon numérateur effrayant: (E²+1)*(E4 +1)*...*(E^2n +1), eh bien si tu effectues en prenant les 3 ou 4 ou 5 ou 6 premiers termes, (en bref les n premiers termes) tu t'aperçois qu'il est chaque fois égal à:
E^2(n-1) + E^2(n-2) + E^2(n-3) +.....+ 1
soit E^(2n) - 1 / E² - 1
Et voilà, le reste ne pose pas de problème...
Bon courage. Ton sérieux pour cet exo et l'autre que tu as résolu m'a impressionné.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités