Un produit classique

[mehdi-128]

Bonjour,

:

J'ai calculé :

Je comprends comment on obtient la relation :



J'ai :

Après je vois pas.

[lynux]

Bonjour,

On a

[hdci]

Une idée :




Puis en exprimant en fonction de : on peut le faire :

• soit en exploitant la formule de la première question (calculer )
  
  
• soit en remarquant que

Il n'y a plus qu'à finir les calculs

[hdci]

@lynux : ah ben on s'est croisé...

[aviateur]

soit en remarquant que

Bonjour
On peut aussi remarquer que le DSE de
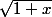
est:
mais aussi

Comme cela donne directement :

Pour finir on utilise la relation en entre et donnée ci-dessus par @hdci.

[aviateur]

mais en fait j'ai pas vu le message de lynux, on peut faire direct comme lui

[mehdi-128]

soit en remarquant que

Bonjour
On peut aussi remarquer que le DSE de
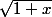
est:
mais aussi

Comme cela donne directement :

Pour finir on utilise la relation en entre et donnée ci-dessus par @hdci.

Merci mais j'en suis au 1er chapitre de MPSI Analyse, donc j'ai pas encore revu les séries entières.

[mehdi-128]

Bonjour,

On a

Merci, le plus rapide

@Hdci

Un peu long et calculatoire votre méthode.

[Kolis]

Bonjour !
On pouvait aussi utiliser

[aviateur]

Merci mais j'en suis au 1er chapitre de MPSI Analyse, donc j'ai pas encore revu les séries entières.

Bonjour, En tout cas tu peux garder cela en mémoire et de toute façon d'autres personnes t'ont donné de solutions