Problème de trou dans un circle

par **mazen.khoder** » 16 Oct 2015, 11:38

Bonjour ,
mon question est :
si on a une transformation dans un circle unité sachant que A est le point (1,0) et initialement un point M est sur le circle d'angle (OA,OM) =Pi + x (x est irrationel) la transformation est M => M' / (OA,OM') = (OA,OM) + Pi + x
alors si on a un trou dans le circle entre le deux points T1 et T2 / (OA,OT1) = - epsilon et (OA,OT2) = + epsilon (x << epsilon ) après combien de steps le point M tombe dans le trou ?
Merci.

par **Kolis** » 16 Oct 2015, 13:42

irrationnel ? Il me semble que si

les images de

sont confondues avec

, donc dans le "trou " dès le départ ou alors jamais !

par **mazen.khoder** » 16 Oct 2015, 13:54

Merci ,
mais x est trés petit et irrationnel c'est a dire on ne peut pas maitre x = Pi *(a/b) ou a et b sont nombres naturelles .

par **mathelot** » 16 Oct 2015, 14:59

la question relève des systèmes dynamiques et de la théorie ergodique.

par **mazen.khoder** » 16 Oct 2015, 15:14

Merci ,
oui je sais, mais je voudrais la solution exact de mon question ...

par **Kolis** » 16 Oct 2015, 16:51

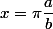
n'a rien à voir avec

irrationnel et très petit !

En revanche, pour

on peut montrer que

est dense dans

ce qui répond à ta question d'existence.
Quelle valeur de

convient, c'est une autre histoire !

par **mazen.khoder** » 19 Oct 2015, 10:01

Kolis a écrit: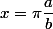 n'a rien à voir avec irrationnel et très petit !

En revanche, pour on peut montrer que est dense dans ce qui répond à ta question d'existence.
Quelle valeur de convient, c'est une autre histoire !

Merci beaucoup , je voudrais encore l'autre histoire

Problème de trou dans un circle

problème de trou dans un circle

Qui est en ligne