Problème sur les réels

[Marillion]

Bonjour à tous,

Voilà l'énoncé:
Soient A et B deux parties de R (R ensemble des reéls).
Montrer que A inclus dans B implique que complémentaire de A est inclus dans complémentaire de B.

[Zebulon]

Bonjour,

Soient A et B deux parties de R (R ensemble des reéls).
Montrer que A inclus dans B implique que complémentaire de A est inclus dans complémentaire de B.

ça va être très difficile à montrer...
C'est dans l'autre sens : .

[Mohamed]

salut

l'énoncé est faux, ca doit etre comme ça
Mq A inclus ds B implique la complémentaire de B inclus ds la complémentaire de A
tu peux démontrer ça en utilisant la contraposée...

[Zebulon]

tu peux démontrer ça en utilisant la contraposée...

La contraposée ? Pourquoi ne pas le démontrer directement ? C'est immédiat !

[Marillion]

En fait, j'ai mal traduit l'énoncé:
Il faut démontrer que A incluse dans B implique adhérence de A incluse dans adhérence de B.
Toutes mes excuses...mais si vous pouviez à nouveau m'aider...

[abcd22]

Qu'est-ce que vous avez vu comme définition de l'adhérence ou propriétés équivalentes à le définition ?

[Zebulon]

Première question : on est dans un espace métrique ou topologique quelconque ?
Ensuite, il faut traduire je le fais dans un espace métrique)
.
On veut montrer que si , alors , ie :
.
Alors on se donne un r>0, et on le montre...

[Marillion]

On se trouve dans un espace topologique.

[Zebulon]

Alors on remplace les boules par des voisinages de x.

[abcd22]

Dans le premier post tu dis A et B parties de pourtant ?

[Marillion]

Merci.
C'étatit tout simple en définitive.

[aviateurpilot]

on sais que:
(P => Q) (non Q => non P)
donc:
( => ) ( => )
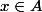
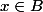
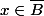
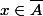
par suite
=>

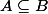
[yos]

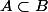
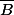
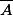
donc . Mais est fermé et est le plus petit fermé contenant A.
Donc.