Probléme sur un calcul d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aminjeb
- Messages: 3
- Enregistré le: 28 Déc 2014, 22:38
-
 par aminjeb » 28 Déc 2014, 22:51
par aminjeb » 28 Déc 2014, 22:51
Salut tout le monde,
J'ai un exercice qui m'a fait bloquer :
Montrer que l'égalité
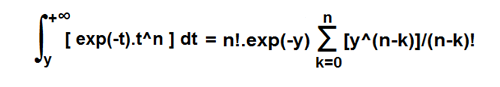
est vrai.
On doit travailler avec intégration par parties. Mais je ne sais pas comment trouver la formule générale de la somme.
Merci
-
eriadrim
- Membre Relatif
- Messages: 113
- Enregistré le: 19 Oct 2013, 12:04
-
 par eriadrim » 29 Déc 2014, 00:05
par eriadrim » 29 Déc 2014, 00:05
Salut,
Procède par récurrence : avec l'intégration par partie, tu te ramène presque immédiatement au cas précédent.
-
aminjeb
- Messages: 3
- Enregistré le: 28 Déc 2014, 22:38
-
 par aminjeb » 29 Déc 2014, 15:58
par aminjeb » 29 Déc 2014, 15:58
eriadrim a écrit:Salut,
Procède par récurrence : avec l'intégration par partie, tu te ramène presque immédiatement au cas précédent.
l'intégration par partie me donne :

e(-t).t^n.dt =[-e(-t).t^n]+......+(n*(n-1)...*2)[-e(-t).t] + (n*(n-1)...*2)*;)e(-t)dt
S'il vous plaît, vous pouvez rédiger la solution?
Merci
-
eriadrim
- Membre Relatif
- Messages: 113
- Enregistré le: 19 Oct 2013, 12:04
-
 par eriadrim » 30 Déc 2014, 10:09
par eriadrim » 30 Déc 2014, 10:09
Si tu pose

et tu veux montrer par récurrence que
!})
On a
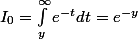
, donc la relation que l'on veut montrer est vrai au rang 0.
Supposons que la relation est vrai pour un

fixé. Dans ce cas :
\int_y^\infty e^{-t}t^ndt)
(intégration par partie)
Donc
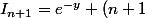I_n = e^{y} + (n+1) \times n! e^{-y}\sum_{k=0}^n \frac{y^{n-k}}{(n-k)!})
Après il faut que tu te ramène à la somme avec n+1 à la place du n. Et tu peux conclure que par récurrence,
!})
-
aminjeb
- Messages: 3
- Enregistré le: 28 Déc 2014, 22:38
-
 par aminjeb » 30 Déc 2014, 17:00
par aminjeb » 30 Déc 2014, 17:00
Merci bien. Ta réponse est suffisante.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
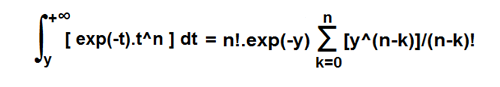 est vrai.
est vrai.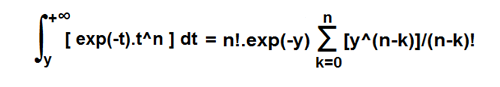 est vrai.
est vrai.