Problème de Somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 16:13
par HagerFall » 01 Oct 2017, 16:13
Bonjour,
Je n'arrive pas à trouver de résonnement qui fonctionne et il faut que j'arrive cette question pour pouvoir commencer mon DM car sans cette question je ne peux pas avancer.
Si quelqu'un pourrait sérieusement m'aider j'en serais ravis.
Montrer que:
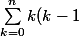\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}=n(n-1)x^2)
(Si la formule ne passe pas désolé essayer de la rentrer dans l'éditeur d'équation).
Modifié en dernier par
HagerFall le 01 Oct 2017, 16:23, modifié 1 fois.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 16:20
par infernaleur » 01 Oct 2017, 16:20
HagerFall a écrit:Bonjour,
Je n'arrive pas à trouver de résonnement qui fonctionne et il faut que j'arrive cette question pour pouvoir commencer mon DM car sans cette question je ne peux pas avancer.
Si quelqu'un pourrait sérieusement m'aider j'en serais ravis.
Montrer que:
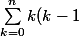\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}=n(n-1)x^2)
(Si la formule ne passe pas désolé essayer de la rentrer dans l'éditeur d'équation).
Ta juste oublier les balises "[tex.]" au début et "[/tex.]" a la fin
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 16:22
par infernaleur » 01 Oct 2017, 16:22
Tu pourrais utiliser cette formule :
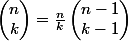
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 16:25
par HagerFall » 01 Oct 2017, 16:25
J'ai essayé pendant des heures avec toutes les formules mais sur l'ensemble je ne retombe jamais sur la bonne solution, je ne sais pas si j'ai fait une erreur de calcul parmi mes test mais je bloque totalement.
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 16:39
par HagerFall » 01 Oct 2017, 16:39
Par exemple je ne sais pas si je suis sur la bonne voie ni comment continuer:
(\frac{(1-x)^n-(1-x)^2^n}{x})\sum_{k=0}^{n}{k(k-1)(\frac{n}{k})\begin{pmatrix}n-1\\k-1 \end{pmatrix})
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 16:39
par infernaleur » 01 Oct 2017, 16:39
Il ne faut pas oublier de sortir les termes pour k=0 et k=1 avant d'utiliser la formule que j'ai énoncé.
tu obtiens donc après avoir sortie les termes pour k=0 et 1 :
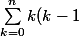\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}<br />=\sum_{k=0}^{1}{k(k-1)\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^{n-k} + \sum_{k=2}^{n}{k(k-1)\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^{n-k}})
Dans la somme qui varie de k=0 à k=1 on obtiens 0, donc on a :
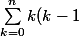\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}=\sum_{k=2}^{n}n(n-1)\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
(J'ai utilisé la formule que je t'avais énoncé)
Pour l'instant il n'y pas de problème ?
Modifié en dernier par
infernaleur le 01 Oct 2017, 17:22, modifié 12 fois.
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 16:47
par HagerFall » 01 Oct 2017, 16:47
AH..... Je ne connais pas cette méthode ni ne la comprend. Je ne vois pas ce que tu a fait.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:07
par infernaleur » 01 Oct 2017, 17:07
Désolé mais je viens de me rendre compte que j'ai fait une grossière erreur !!!
C'est plutôt sa :
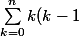\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}=\sum_{k=2}^{n}n(n-1)\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
(j'ai modifié mon ancien message)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:13
par infernaleur » 01 Oct 2017, 17:13
infernaleur a écrit:Il ne faut pas oublier de sortir les termes pour k=0 et k=1 avant d'utiliser la formule que j'ai énoncé.
tu obtient donc après avoir sortie les termes pour k=0 et 1 :
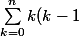\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}<br />=\sum_{k=0}^{2}{k(k-1)\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^{n-k} + \sum_{k=2}^{n}{k(k-1)\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^{n-k}})
Dans la somme qui varie de k=0 à k=2 on obtiens 0 donc on a :
On obtiens donc
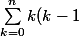\begin{pmatrix}n\\k \end{pmatrix}(x^k)(1-x)^n^-^k}=\sum_{k=2}^{n}n(n-1)\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
(J'ai utilisé la formule que je t'avais énoncé)
Pour l'instant il n'y pas de problème ?
Dit moi quand pour ce passage c'est bon
Modifié en dernier par
infernaleur le 01 Oct 2017, 17:37, modifié 1 fois.
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 17:14
par HagerFall » 01 Oct 2017, 17:14
infernaleur a écrit: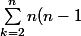\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
Soit:
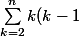(\frac{n}{k})(\frac{n}{k})\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:16
par infernaleur » 01 Oct 2017, 17:16
HagerFall a écrit: infernaleur a écrit: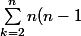\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
Soit:
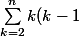(\frac{n}{k})(\frac{n}{k})\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
?
Attention c'est
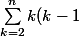(\frac{n}{k})(\frac{n-1}{k-1})\begin{pmatrix}n-2\\k-2 \end{pmatrix}x^k(1-x)^{n-k})
Modifié en dernier par
infernaleur le 01 Oct 2017, 17:17, modifié 1 fois.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:16
par infernaleur » 01 Oct 2017, 17:16
Oui sinon j'ai bien utilisé sa pour trouver ma formule, et c'est pour sa d'ailleurs que j'ai enlever les termes de la somme pour k=0 et k=1 parce que sinon on aurait divisé par 0 ce qui pose problème ...
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 17:19
par HagerFall » 01 Oct 2017, 17:19
..
Modifié en dernier par
HagerFall le 01 Oct 2017, 17:27, modifié 1 fois.
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 17:20
par HagerFall » 01 Oct 2017, 17:20
Ok, je comprend jusqu'à là.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:21
par infernaleur » 01 Oct 2017, 17:21
HagerFall a écrit:Enfaîte c'est plus simple c'est juste que la somme de 0 à 2 on a k(k-1) et pour la somme de 2 à n on a la même chose, on a alors l'équivalent de n(n-1) ?
la somme de 0 à 1 !!!
après j'ai pas compris ce que tu voulais dire, comment sa pour la somme de 0 à 1 on a k(k-1) ?
Et comment sa pour la somme de 2 à n on a un équivalent de n(n-1) ?
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 17:26
par HagerFall » 01 Oct 2017, 17:26
J'ai rien dit.... Chuuuuut

-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:33
par infernaleur » 01 Oct 2017, 17:33
D'accord ^^
Bref arriver à la pour utiliser la formule du binôme, on devrai faire apparaitre une somme qui varie de 0 à n-2 et un coefficient binomial de cette forme :

au lieu de

Ainsi on va faire un changement d'indice pour que la somme ne varie plus de 2 à n mais de 0 à n-2.
Pour cela on pose i=k-2 (on voit bien qu'on va faire ce changement de variable pour modifier comme on le voulait le coefficient binomial)
Comme

bha on a

Donc ainsi en respectant ce changement d'indice dit moi que deviens la somme ?
-
HagerFall
- Membre Naturel
- Messages: 24
- Enregistré le: 01 Oct 2017, 15:42
-
 par HagerFall » 01 Oct 2017, 17:44
par HagerFall » 01 Oct 2017, 17:44
Avec i=k-2
et k=2 on a k=i soit k=2-2=0 et n-2
\begin{pmatrix}n-2\\i \end{pmatrix}x^k(1-x)^{n-k})
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:51
par infernaleur » 01 Oct 2017, 17:51
HagerFall a écrit:Avec i=k-2
et k=2 on a k=i soit k=2-2=0 et n-2
\begin{pmatrix}n-2\\i \end{pmatrix} x^k(1-x)^{n-k})
Attention i=k-2 =>k=i+2 donc il faut changer aussi les x^k et x^n-k !!!
Donc c'est plutôt sa :
\begin{pmatrix}n-2\\i \end{pmatrix} x^{i+2}(1-x)^{n-i-2})
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 01 Oct 2017, 17:52
par infernaleur » 01 Oct 2017, 17:52
Maintenant à toi de voir qu'est-ce que tu peux faire sortir de la somme pour reconnaître une joli formule du binôme et tu auras fini.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
