Probleme de récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
par lomdefer » 14 Oct 2006, 14:41
Cei est la deuxième partie d'un exo.
voici ma conjecture:
 = n)
Donc
 = k)
Mais je ne sais pas quel raisonnement par recurrence utilisé car on a plusieur variante dans le cour.
1.
On prend n=0, j'ai déja prouver dans la deuxième aprtie de l'exo que
=0)
donc ona
)
qui est vraie.
Mais après pour le n+1 je ne sais pas comment faire quelqu'un pourrait me donner une piste ??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 14 Oct 2006, 14:46
Tu ne sais rien d'autre sur f ? (monotonie, bijective ...?)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 14 Oct 2006, 15:23
Salut, tu sais don déjà que f(n)=n pour tout entier naturel n, c'est ça ?
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
par lomdefer » 14 Oct 2006, 15:35
ben non c'est ce que je veux prouver.
En prenant plusieur valeur pour n j'ai simplement conjecture, etma conjecture c'est que f(n) = n.
Et mon prof ma dit que donc mon jypothèse de recurrence devrait etre :
=k)
Et je n'arrive pas a faire la recurrence quandje doit montrer que f(n+1)=n+1
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 14 Oct 2006, 15:55
tu oublies la condition
\leq)
x pour tout
, elle est très importante...
- Tu sais que
=k)
pour tout
Comment montrer que f(n+1)=n+1...?
C'est simple, d'après ce que je t'ai rappelé au tout début, on a nécessairement :
\leq n+1)
donc
\in\{0,1,2,\cdots,n,n+1\})
mais comme les premières valeurs
sont déjà prisent par
,f(1),\cdots,f(n))
, il n'y a plus qu'une possiblité :
=n+1)
.
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
par lomdefer » 14 Oct 2006, 17:10
j'ai u probleme avec un autre recurrnce si sa ne te dérange pas...
Montrer par recurrence que
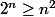
pour tout
.
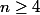
Alors déja je fait l'initialisation.
pour n=4 on a
donc
)
est vraie.
Maintenant je suppose
)
vraie.
on a donc
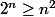
et je veux obtenir que
^2)
comment je fais ??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 14 Oct 2006, 17:26
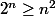
donc
. De plus
^2 = n^2+2n+1)
reste à montrer que
...
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
par lomdefer » 14 Oct 2006, 17:48
franchement j'arive pas a montrer que
^2)
il faut dire que , déja
, que
et que 2
donc
??
FRANCHEMENT JE VOIS PAS COMMENT FAIRE...
par sandrine_guillerme » 14 Oct 2006, 18:07
je crois que c'est simple .. calcul la différence
ensuite manipules les identité remarquables .. et remarque qu'a droite c'est le début d'un identité remarquable 1 après la 3 ..
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
par lomdefer » 14 Oct 2006, 18:31
Ben si je fait :
^2)
=
)
=
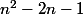
et
^2 - 2)
donc
^2=(n-1)^2 - 2)
comme ici on cherche P(n) vrai pour tout n >= 4 alors
^2-2 > 0)
donc
et donc
c'est bon sa ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 14 Oct 2006, 18:34
Oui c'est bon :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
