Bonjour, actuellement en prepa scientifique je n'arrive pas à répondre à cette question :
Déterminer toute les fonctions f : R×R->R qui vérifient:
D correspond au dérivé partielle
D^2f/Dx^2(x,y)+4Df/Dx(x,y)+13f(x,y)
=13xy^2+13x^2+8x+2
Et pour tout y appartenant à R on a f(0,y)=-4/13y^2
Merci d'avance pour votre aide
Problème en rapport avec dérivé partielle
7 messages
- Page 1 sur 1
Re: Problème en rapport avec dérivé partielle
Bonjour,
Tes dérivées partielles ne sont que par rapport à x. Tu peux donc considérer cette équation comme une équation différentielle (linéaire) du second ordre, en x....
Est ce que ça t'aide à avancer?
Tes dérivées partielles ne sont que par rapport à x. Tu peux donc considérer cette équation comme une équation différentielle (linéaire) du second ordre, en x....
Est ce que ça t'aide à avancer?
Re: Problème en rapport avec dérivé partielle
Il s'agit en effet d'une équa diff paramétrée par y et selon les valeurs du paramètre y , les solutions sont de telle ou telle forme...
Re: Problème en rapport avec dérivé partielle
Bonjour,
on cherche les solutions de l'équation homogène}{\partial x^2}+4 \dfrac{\partial f(x,y)}{\partial x}+13 f(x,y)=0) (*)
(*)
L'équation associée, d'inconnue z, est

qui a pour solutions:

La solution générale de l'équation (*) sans second membre est:
 = (A(y) cos(3x)+B(y) sin(3x))e^{-2x}) où A et B sont des fonctions quelconques
où A et B sont des fonctions quelconques
de la variable .
.
on cherche les solutions de l'équation homogène
L'équation associée, d'inconnue z, est
qui a pour solutions:
La solution générale de l'équation (*) sans second membre est:
de la variable
Modifié en dernier par mathelot le 17 Nov 2022, 12:28, modifié 2 fois.
Re: Problème en rapport avec dérivé partielle
L'équation avec second membre s'écrit
}{\partial x^2}+4 \dfrac{\partial f(x,y)}{\partial x}+13 f(x,y)= 13x^2+x(13y^2+8)+2) (**)
(**)
On cherche une solution particulière g de l'équation avec second membre sous la forme:
=A(y)x^2+B(y)x+C(y))
=2A(y)x+B(y))
=2A(y))
où A,B,C sont des polynômes de la variable y.
On remplace f par g dans l'équation (**)
+8A(y)x+4B(y)+13A(y)x^2+13B(y)x+13C(y)=13x^2+x(13y^2+8)+2)
on identifie les deux membres:
=13)
=1)
+13B(y)=13y^2+8)
=13 y^2)
=y^2)
+4B(y)+13C(y)=2)
=0)
= - \dfrac{4}{13}y^2)
Au final, on trouve:
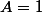 et
et  et
et 
La solution générale de l'équation (avec second membre) est:
=(A(y)cos(3x)+B(y)sin(3x))e^{-2x}+x^2+xy^2-\dfrac{4}{13}y^2)
où A et B sont des fonctions quelconques de la variable y.
On cherche une solution particulière g de l'équation avec second membre sous la forme:
où A,B,C sont des polynômes de la variable y.
On remplace f par g dans l'équation (**)
on identifie les deux membres:
Au final, on trouve:
La solution générale de l'équation (avec second membre) est:
où A et B sont des fonctions quelconques de la variable y.
Re: Problème en rapport avec dérivé partielle
La solution générale de l'équation (avec second membre) est:
=(A(y)cos(3x)+B(y)sin(3x))e^{-2x}+x^2+xy^2-\dfrac{4}{13}y^2)
où A et B sont des fonctions quelconques de la variable y.
Avec la condition initiale=-\dfrac{4}{13}y^2)
il vient:
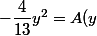 -\dfrac{4}{13}y^2)
=0)
Les solutions de l'équation, avec second membre, sont de la forme:
=B(y)sin(3x) e^{-2x}+x^2+xy^2-\dfrac{4}{13}y^2)
où A et B sont des fonctions quelconques de la variable y.
Avec la condition initiale
il vient:
Les solutions de l'équation, avec second membre, sont de la forme:
Re: Problème en rapport avec dérivé partielle
Matt2000d a écrit:Et pour tout y appartenant à R on a f(0,y)=-4/13y^2
On a besoin d'une deuxième condition initiale pour déterminer B(y).
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
