Problème preuve mathématique

[Guillermo]

Bonjour à tous, ∈
Je n'arrive pas à terminer une preuve mathématique....
Soient les sous-ensembles non vides A et B de R et soit C l'ensemble C = {a + b | a ∈ A, b ∈ B} . Je dois prouver que si chacun de A et de B ont un infimum (terme anglais), alors C a un infimum, et inf C = inf A + inf B.
Voici deux théorèmes que je suis censé utiliser pour ma preuve :
Théorème n°1 : Soit h un nombre positif donné et soit S un ensemble des nombre réels. Si S a un infimum, alors pour un certain x dans S nous avons x < inf S + h.
Théorème n°2 : Si trois nombres réels a, x et y satisfont les inégalités a ≤ x ≤ a + y/n pour chaque entier ≥ 1, alors x = a.
Mon début de preuve :
1) Supposons que chacun de A et de B ont un infimum. Puisque, par définition, inf X est une borne inférieure de X, alors inf X ≤ x pour tout x dans X. Par conséquent, inf A ≤ a pour tout a dans A et inf B ≤ b pour tout b dans B.
2) Par définition de C, si c ∈ C, alors c = a + b où a ∈ A et b ∈ B.
3) Par la formule "si x < y et si w < z, alors x + w < y + z", on a donc inf A + inf B ≤ a + b.
4) Comme c = a + b, on a inf A + inf B ≤ c.
5) Par définition de la borne inférieure, on remarque que inf A + inf B est une borne inférieure de C.
6) Comme à la fois C est non vide et C a une borne inférieure*, alors selon le "greatest-lower-bound property", C possède possède un infimum (autrement dit C possède "la plus grande borne inférieure").
7) Comme, par définition de l'infimum, M ≤ inf X pour toute borne inférieure M de X, alors inf A + inf B ≤ inf C.
8) Maintenant, soit n un entier positif quelconque. Par le Théorème n°1 (avec h = 1/n), il existe un a dans A et un b dans B tel que a < inf A + 1/n et b < inf B + 1/n.
9) Par la formule "si x < y et si w < z, alors x + w < y + z", on a donc a + b < inf A + inf B + 2/n.
10) On a donc a + b - 2/n < inf A + inf B et puisque inf C ≤ a + b, on a donc inf C - 2/n ≤ a + b - 2/n.
11) Nous avons inf C - 2/n ≤ a + b - 2/n < inf A + inf B.
12) Enfin, puisque on a inf A + inf B ≤ inf C et puisque on a inf C - 2/n ≤ a + b - 2/n < inf A + inf B, nous avons inf C - 2/n < inf A + inf B ≤ inf C. Et puis là, je bloque...
Merci de m'avoir lu et merci beaucoup de votre aide !!
*Edit : j'avais à tort écrit "Comme à la fois C est non vide et C a une borne supérieure", je le remplace par "Comme à la fois C est non vide et C a une borne inférieure"

[catamat]

Bonjour
D'après le point 11)

Nous avons inf C - 2/n ≤ a + b - 2/n < inf A + inf B.

On en déduit que pour tout entier n non nul
inf C ≤ inf A + inf B +2/n

Le théorème 2 alors permet de conclure

[Guillermo]

Merci ! C'était simple, en fait... Mais j'écrirais plutôt inf C < inf A + inf B +2/n au lieu de inf C ≤ inf A + inf B +2/n, tu ne trouve pas ?

[Ben314]

Salut,
C'est long, compliqué et à certains endroit passablement faux : le point 6) c'est n'importe quoi vu que rien ne dit que C admet une borne supérieure et que, même si c'était le cas, ça n'aurait évidement aucune conséquence concernant le fait que ce même ensemble C admette ou pas une borne inférieure.

Tu doit montrer que, si et sont deux parties non vide de admettant des bornes inférieures et alors admet une borne inférieure qui est .
Et la seule chose dont tu as besoin, c'est de la définition d'une "borne inférieure" : la borne inférieure d'un ensemble c'est le plus grand minorant de l'ensemble (qui peut ne pas exister).
Donc DEUX chose à démontrer (et pas 36...) :

(1) est un minorant de :
Soit un élément quelconque de . Il peut s'écrire (par définition de ) avec et .
Par définition et sont des minorants de et de donc et .
Donc .

(2) Il n'y a pas de minorant de qui soit strictement plus grand que :
Soit un réel quelconque strictement plus grand que .
On a qui est le plus grand minorant de donc n'est pas un minorant de ce qui signifie qu'il existe un tel que .
On a qui est le plus grand minorant de donc n'est pas un minorant de ce qui signifie qu'il existe un 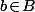tel que .
On a donc avec (par définition de ) donc n'est pas un minorant de .

[Guillermo]

Merci pour ta réponse,
Pour le point 6 : je me suis trompé en écrivant ! Du coup j'ai modifié le "Comme à la fois C est non vide et C a une borne supérieure" et je l'ai remplacé par "Comme à la fois C est non vide et C a une borne inférieure".
C'est mon livre qui m'a demandé d'utiliser les deux théorèmes susmentionnés pour réaliser cette preuve...
Concernant la 1re partie de ta preuve :
Je ne comprends comment tu arrives à c = a + b ≤ α + β... Puisque α ≤ a et β ≤ b, j'aurais plutôt dit au contraire que α + β ≤ a + b = c !
Concernant la 2e partie de ta preuve :
Je n'ai pas compris comment tu arrives à ta dernière ligne : je ne vois pas en quoi le fait que γ soit supérieur à a + b implique que γ n'est pas un minorant de C...
Par ailleurs tu auras remarqué que j'ai besoin que *toutes* les étapes d'une preuve soient mentionnées sinon je ne comprends pas... D'habitude beaucoup d'étapes sont passées ou sous-entendues, c'est pour cela que souvent je ne comprends pas...