Bonjour à tous,
Le problème d'optimisation que j'ai à résoudre est le suivant. Je dois déterminer un vecteur
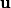
tel que, idéalement :
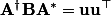
où
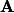
et
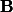
sont connues, et

,

et

dénotent respectivement la transposition, transposition-conjugaison et conjugaison. En pratique, les matrices
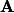
et
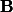
sont bruitées tel que
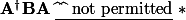
ne puisse être exprimée directement par un simple produit
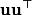
.
Le problème que j'aimerais résoudre serait donc de déterminer un vecteur
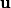
tel que
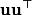
se rapproche le plus possible de
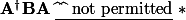
, au sens d'un certain critère. Par exemple, en posant
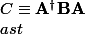
, j'ai pensé à la construction d'une fonction objective
$)
de la forme :
=\bf{p}^\dag(\bf{C}-\bf{u}\bf{u}^\top)\bf{p}$)
Le problème consisterait alors à déterminer
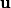
qui minimise
|^2)$)
. L'ennui est que, mis à part de façon itérative et numérique, je ne parviens pas à résoudre ce problème de façon analytique directement en fonction de
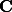
, ce que j'aimerais bien faire.
Quelqu'un saurait-il comment s'y prendre?
Merci beaucoup ; )
