un coffre de cèdre a une longueur qui est le double de sa largeur. le coût de fabrication du couvercle par dm^2
est 4 fois celui par dm^2 du reste du coffre. Si le volume du coffre est de 1440 dm^3, trouve les dimensions qui minimisent le coût de fabrication du coffre.
Problème optimisation mathématique
4 messages
- Page 1 sur 1
Re: problème optimisation mathématique
Salut,
C'est plutôt d'un (petit) niveau Lycée que supérieur (simple étude de fonction) :
(1)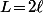
(2) Le cout est proportionnel à :
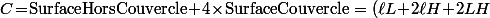\!+\!4\!\times\!\ell L\mathop{=}\limits_{(1)}10\ell^2\!+\!6\ell H)
(3)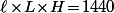 donc
donc 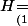}\!\dfrac{720}{\ell^2}) et
et 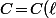\!=\!10\ell^2\!+\!\dfrac{6\!\times\!720}{\ell})
-> Dérivée + Tableau de variation + Conclusion.
C'est plutôt d'un (petit) niveau Lycée que supérieur (simple étude de fonction) :
(1)
(2) Le cout est proportionnel à :
(3)
-> Dérivée + Tableau de variation + Conclusion.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
