Probleme noyau et polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 03 Nov 2007, 16:24
par flofun » 03 Nov 2007, 16:24
Bonjour,
j ai un petit souci je ne sais pas trop comment m y prendre:
f(Q)= (2X+1)Q(X)-(X^2-1)Q'(X)
On a précédemment prouvé que f est un endomorphisme
Déterminer son noyau ker(f)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Nov 2007, 16:31
par tize » 03 Nov 2007, 16:31
Bonjour,
f(Q)=0 ça ressemble à une équation différentielle, non ?
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 03 Nov 2007, 16:34
par flofun » 03 Nov 2007, 16:34
eeuuu ché pas trop
en fait à chaque Q appartenant à R2[X] on associe le polynome f(Q)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Nov 2007, 16:35
par tize » 03 Nov 2007, 16:35
Q est un polynôme de degré 2 ? Ba fallait le dire !
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 03 Nov 2007, 16:38
par flofun » 03 Nov 2007, 16:38
dsl lol
j suis allé un peu vite ds ma redaction
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Nov 2007, 16:47
par tize » 03 Nov 2007, 16:47
Dans ce cas, tu peux poser
=ax^2+bx+c)
dériver et regarder ce qui ce passe en identifiant les coefficients dans
Q(X)-(X^2-1)Q'(X)=0)
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 03 Nov 2007, 16:51
par flofun » 03 Nov 2007, 16:51
ok merci
je vais essayer ça !
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 05 Nov 2007, 14:18
par flofun » 05 Nov 2007, 14:18
par contre, là je bloque.
J ai dérivé Q(X), j ai remplacé dans l'équation en essayant d'identifier les coefficients mais je ne vois pas trop quoi tirer de cette équation. :hum:
-
SimonB
 par SimonB » 05 Nov 2007, 14:22
par SimonB » 05 Nov 2007, 14:22
Tu as deux polynômes (0 et le truc à gauche dans ton équation) qui coïncident sur

donc sont égaux ; donc, tu peux identifier les coefficients : terme constant, terme en X, terme en
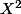
... Tu en tires des équations sur tes paramètres a, b, c, et tu en déduis ton noyau.
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 05 Nov 2007, 14:36
par flofun » 05 Nov 2007, 14:36
Bonjour
merci beaucoup
je trouver ker(f) = (vecteur nul)
Cela signifie-t-il que f est bijectif ?
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 05 Nov 2007, 15:16
par flofun » 05 Nov 2007, 15:16
est-ce que je me trompe ?
-
Alex29
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Nov 2007, 12:43
-
 par Alex29 » 05 Nov 2007, 15:36
par Alex29 » 05 Nov 2007, 15:36
Non non tu as raison :we:
Car tu as un endomorphisme, allant d'un espace de dimension finie dans un espace de même dimension, et injectif.
tu as bien l'équivalence injectif bijectif
C'est donc un automorphisme :++:
-
flofun
- Membre Naturel
- Messages: 25
- Enregistré le: 02 Nov 2007, 12:03
-
 par flofun » 05 Nov 2007, 15:48
par flofun » 05 Nov 2007, 15:48
ok
merci beaucoup !
-
Alex29
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Nov 2007, 12:43
-
 par Alex29 » 05 Nov 2007, 15:53
par Alex29 » 05 Nov 2007, 15:53
de rien :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
