Problème de maximum

[Sara1999]

Bonjour,
Je n’arrive pas à montrer que 3/4 est le maximum de :
1/(x+3) + 1/(y+3) + xy/(1+3xy)
x et y deux réels strictement positifs.
Bien sûr pour x=y=1 on a bien l’égalité.
Merci .

[GaBuZoMeu]

Bonjour,
As-tu fait la recherche des points critiques de la fonction sur le quadrant positif ?

[Sara1999]

Pour la recherche des points critiques, j’ai trouvé:(x=y=1/9 )ou (x=1/9 et y=81 )ou (x=81 et y=1/9 ) ou (x=y=1)
Mais je ne sais pas comment continuer .
Merci.

[GaBuZoMeu]

Il faudra de toutes façons faire attention à ce qui se passe aux bords du domaine. Tu peux commencer par évaluer la fonction aux points critiques que tu as trouvés (je n'ai pas vérifié tes calculs).

[Black Jack]

Bonjour,

Les points critiques trouvés sont corrects.

[Sara1999]

Merci d’avoir confirmé ma recherche des candidats d’extremums, j’ai pu aussi éliminer tous les autres cas et ne laisser que (1,1). Il me reste à montrer qu’il s’agit bien d’un extremum global et non seulement local. Merci de m’aider à voir pourquoi.
J’ai pensé à étudier la fonction f(x,x), la dériver et obtenir x=1 . Est ce la bonne piste ou bien je m’égare ?

[GaBuZoMeu]

Ce que tu suggères ne règle pas le problème du comportement de la fonction quand on tned vers le bord du domaine. elle pourrait dépasser la valeur 3/4 en tandant vers le bord, sans qu'il y ait de point critique.

[Sara1999]

Effectivement je m’en suis rendue compte, à présent je me suis arrêtée au point suivant:
Il faut montrer que 5x^2y^2+3x^2y+3xy^2-24xy+5x+5y+3>=0 mais je n’arrive pas à faire apparaitre la somme des carrés à l’aide d’identités remarquables.

[GaBuZoMeu]

Tu ne peux pas forcément espérer faire apparaître une somme de carrés : déjà il y a à tenir compte du fait qu'on est sur le quadrant positif, et ensuite un polynôme positif partout n'est pas forcément une somme de carrés.
À mon avis, pas d'autre voie que d'examiner ce qui se passe au bord : sur le demi-axe des positif, sur le demi-axe des positif, et à l'infini (c'est le plus délicat).

[Black Jack]

Bonjour,

Aux sottises près (bien possibles),

il me semble que si une des 2 variables --> +oo (avec l'autre > 0), c'est assez immédiat.

1/(x+3) + 1/(y+3) + xy/(1+3xy)

Supposons y --> +oo
On a alors : 1/(y+3) --> 0
et xy/(1+3xy) --> 1/3
alors que 1/(x+3) <= 1/3

et donc pour y --> +oo, on a 1/(x+3) + 1/(y+3) + xy/(1+3xy) <= 1/3 + 0 + 1/3
on a 1/(x+3) + 1/(y+3) + xy/(1+3xy) <= 2/3 (et a fortiori < 3/4)

Reste évidemment les cas où aucune des variables ne tend vers +oo

[GaBuZoMeu]

Une affirmation un peu hâtive : "si y-> +oo, alors xy/(1+3xy) -> 1/3"
Mais ce n'est pas grave, on a toujours sur le quadrant positif xy/(1+3xy) <= 1/3.
Je suggère qu'on laisse Sara1999 réfléchir ...

[Black Jack]

Si y --> +oo avec x > 0, alors (x*y) --> +oo

et en posant x*y = A, on a lim(A-->+oo) [A/(1 + 3A)] = 1/3

et avec f(A) = A/(1 + 3A) , f'(A) > 0 et donc f est croissante.

Donc xy/(1+3xy) <= 1/3 (pour y --> +oo et x > 0)

[GaBuZoMeu]

En restant dans le quadrant positif, on peut très bien avoir y tendant vers plus l'infini avec xy constant, égal à 1/1000 par exemple ; auquel cas xy/(1+3xy) tend vers 1/1003. Ton affirmation est donc bien hâtive.
Mais je le répète, ça n'a pas d'importance car on a toujours xy/(1+3xy) <= 1/3 sur le quadrant positif.

[Sara1999]

Je suis un peu perdue, est ce que vous pouvez me récapituler ce que je dois démontrer précisément . Désolée pour le dérangement .

[GaBuZoMeu]

Je te suggère de montrer que le maximum de ta fonction sur un carré est bien 3/4 atteint au point (1,1) que tu as trouvé et que la fonction est <3/4 sur la partie du quadrant poqitif à l'extérieur de ce carré. Il convient de bien choisir le .

[tournesol]

Cet exercice peut être résolu par des moyens élémentaires:
On considère y comme un paramètre et on étudie les variations de f(x,y) pour y fixé.
MAIS ATTENTION: LA MÉTHODE QUE TE PROPOSE GaBuZoMeu EST PLUS RAPIDE ET BIEN PLUS ÉLÉGANTE .
J'étudie les variations de f en fonction de x lorsque y=k .
k est fixé dans et x décrira
Je pose

Le dénominateur est clairement strictement positif pour les valeurs autorisées pour x et k .
Le numérateur s'annule en
Pour k=0 est strictement décroissante . Elle atteint son max pour x=0 soit
Cette valeur est inférieure à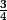
pour est strictement décroissante sur puis strictement croissante sur


Compte tenu de ses variations , cette valeur commune est le max de
Pour , est constante et prend la valeur qui est inférieure à
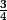
Pour est strictement croissante sur puis strictement décroissante sur
atteint donc son max en et il vaut:

On doit maintenant étudier les variations des deux max obtenus sur leurs intervalles de définition afin de montrer que le "max des max" est inférieur ou égal à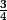
Par exemple est strictement décroissant sur
Il atteint son max pour x=0 soit
Cette valeur est inférieure à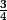
Quant à l'autre max , il est fonction de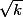
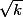définit une fonction croissante de k .
Tu peux donc poser puis dériver. Attention au domaine d'étude de t . Bon courage.