Problème de maximisation

[youbix]

Bonjour, tout d'abord je me présente, Hubert Etudiant en Licence d'économie.
J'ai donc un problème au niveau de la maximisation sans et avec contraintes. A cause des récentes grève je n'ai pas eu ce cours qui pourtant m'interesse vu son utilité pour mes autres matières.
Je ne cherche bien évidement pas de solution a mes problèmes juste la façon dont il faut procédé de manière géneral. Merci d'avance


1er cas
Trouver les solutions X* réelles (x>5) maximisant la fonction f(x)=-sqrt(x-5)
Je me doute donc bien que la solution est 5,000...1 mais je ne sais pas comment écrire cela de manière mathématique.

2ème cas
Trouver les couple solutions de réels (x*,y*) maximisant la fonction f(x,y)=3xy-x^3-y^3
Et je n'ai jamais vu qqch comme sa. Je n'ai donc aucune idée de comment procédé et les articles trouvés sur internet sont assez complexe.
Je pense devoir procédé à l'aide des dérivé partiels et d'une matrice Hessienne mais après plus clairement??
Comment parvenir au couple ?
Merci d'avances.

[fatal_error]

salut,

pour la 1 :
f(x) est strictement decroissantee, continue et définie sur
Elle admet donc un maximum en .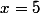
Comme on te dit de trouver les solutions, c'est pas facile, car pour n'importe quel x donné, tu trouveras toujours un tel que . Il suffit de prendre

Pour le deuxieme cas :
Il me semble effectivement qu'il faut calculer une hessienne :

Par symetrie,


On a donc


Pour les points critiques :

Soit pour avoir (1) et (2) y=y^4 en substituant x de (1) par y^2 de (2)
On impose y != 0
et on obtient y^3=1 soit y=1 => x=1

Si y = 0, on a x=0 qui est aussi solution.
Deux points critiques : (1,1) et (0,0)
En (1,1), on remplace dans la matrice Hessienne :

Sur wiki ca dit de chercher les valeurs propres. En fait, on est pas obligé de se taper du pour les trouver.
On sait que la trace de H, c'est la même dans une autre base, pareil pour le déterminant.
On peut donc deduire et
Autrement dit, les deux valeurs propres sont négatives

D'apres wiki, on a donc H definie négative implique (1,1) est un maximum local.
Pour (0,0) même raisonnement (pe pas même resultat)

[youbix]

Merci pour cette réponse très clair.
Je crois comprendre pour la 2, mais pour la 1 je ne vois donc pas comment formuler cela je ne peut pas dire s={5,0000000..1} il doit bien y avoir un terme mathématique pour dire cela non?
ou s=Xmin>5 ? je ne pense pas..
Merci encore pour la 2

[fatal_error]

re,

en fait, je pense que pour le 1 il n'y a pas de solutions qui maximisent f. Car si tu poses x_1=5,2 et que tu dis que c'est une solution, c'est faux : x_2 = 5,1 donne f(x_2)>f(x_1).

[youbix]

Merci beaucoup fatal error pour avoir pris le temps de me répondre. A bientôt !