Problème de matrice: coefficients...

[kira_shinigami]

Bonsoir tout le monde,

Je voulais vous demander si vous connaissez un moyen afin de multiplier chaque ligne d'une matrice par un coefficient différent.

Ce n'est en effet pas une simple multiplication matricielle.

Exemple :

disons que nous avons la matrice A :

[a b c
d e f
g h i]

et j'aimerais avoir une autre matrice contenant 3 coefficients différents (x, y et z) de telle manière que je puisse obtenir en résultat :

R =

[a*x b*x c*x
d*y e*y f*y
g*z h*z i*z]

Quelqu'un aurait-il une idée afin d'obtenir ce résultat par une multiplication de type matricielle ? (du type A*... = R)

Je vous remercie d'avance pour votre aide. J'y ai réfléchi depuis un bon bout de temps sans trouver de réponse à ma question.

Merci d'avance! :we:

Ryo


PS: Actuellement, la seule solution que j'ai trouvé est de multiplier la matrice trois fois, chaque fois par un coefficient unique et prendre la première ligne et après la 2ème ligne et après la 3ème ligne etc... :triste:

[Nightmare]

Salut,

Je dirais (multiplication à gauche) . Pourquoi d'après toi?

[kira_shinigami]

Merci Nightmare pour ta réponse si rapide.

En effet, en multipliant de cette manière,
j'obtiens
x*a + 0*b + 0*c pour le premier membre de la première ligne.
J'avais pensé à faire une opération dans la même idée mais en faisant toujours A* quelque chose. D'où le fait que je n'arrivais pas à résoudre ce casse tête.

De plus, je viens de me rendre compte qu'il s'agirait d'une matrice identité dont chaque ligne est multipliée par un coefficient différent.

En tout cas, merci beaucoup de ta réponse et instructive.
J'espère l'avoir bien saisi.

Ryo

[Nightmare]

En fait, en dehors de voir ça juste comme un calcul de matrice, il s'agit avant tout d'endomorphismes de l'espace. Le fait de multiplier la première ligne de la matrice par x, cela revient à multiplier par x l'abscisse de l'image de chaque vecteur par notre endomorphisme, ou autrement dit, de composer notre endomorphisme avec l'homothétie de rapport k suivant le vecteur (premier vecteur de la base d'origine). Cette homothétie a évidemment pour matrice diag(x,1,1).

Comprends-tu mieux le résultat final?

[Mathusalem]

Sauf que Nightmare, ta matrice multiplie l'image du premier vecteur de base par x, l'image du second par y, l'image du troisieme par z, si je ne m'abuse.

Ainsi, on obtiendrait :

(ax by cz
dx ey fz
gx hy iz)

non ?

[Mathusalem]

J'ai fait un petit calcul :

A la matrice a b c d e f g h i
B la matrice i j k l m n o p q r

et AB = C
où C la matrice ax bx cx dy ey fy gz hz iz


je trouve les equations suivantes :

aj + bm + cp = az
ak + bn + cq = bx
al + bo + ck = cx
dj + mc + fp = dy
dk + en + fq = ey
dl + co + fk = fy
gj + hm + ip = gz
gk + hn + iq = hz
gl + ho + ck = iz

Bonne résolution, si tant est qu'il y en a une :)

[fatal_error]

Salut,

Sauf que Nightmare, ta matrice multiplie l'image du premier vecteur de base par x, l'image du second par y, l'image du troisieme par z, si je ne m'abuse.

(Nightmare précise multiplication par la gausse)

Sinon, si on s'entete par la droite,
on peut mettre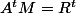 , avec M la matrice de nightmare, puis prendre la transposée sur les deux membres, cqui revient au même vu que avec 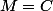, symetrique, et 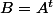, avec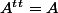

sinon, ben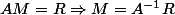 , sous réserve que A inversible

[Mathusalem]

Ah oui, tu as raison, j'ai pas lu "gauche" ..

Sinon par la droite, c'est vrai que ta solution est largement plus agréable.

A+