Probleme de Limite

[shyne99]

Bonjour, voila j'ai une limite qui me prend la tete depuis longtemps et j'arrive pas a la resoudre, donc je viens demander de l'aide ici.......



Merci d'avance parce que je galere comme un fou la .

Au cas ou c'est pas trop visible ça donne ça


Avec Maple je trouve pour limite

[raito123]

biensûr qu'il faut faire entrer l'exp et ln

[shyne99]

Ben j'ai essayer en faisant cela mais sans resultat, de plus je vois pas comment on peut faire ressortir une racine a la limite avec cette expression la

[raito123]

Moi aussi je ne vois pas comment!
pour faire sortir la racine il faut avoir une forme tel que

[shyne99]

j'imagine bien mais le truc c'est que j'ai retourner la formules dans tout les sens et impossible de retrouver une forme du type enfin je chui vraiment larguer sur cette limite.

[tize]

Bonjour,
je dis peut être une grosse bêtise, mais à mon avis on peut peut être majorer et minorer, je m'explique :
avec la concavité du ln on a tout de suite :
et donc:

Reste à majorer...mais c'est peut être une fausse piste...je suis fatigué je vais me coucher, bon courage :we:

[busard_des_roseaux]

bjr,

on prend le log

[Culioli]

Si a est > 0, on a bien, pour x très petit positif
un développement limité du style

a^x = exp[x Ln(a)] = 1 + x Ln(a) + (x^2 )/2 Ln(a)^2 +...

Quand on va reprendre le Ln... en poursuivant le dév limité,...

enfin, ce me semble...

[tize]

Bah oui Busard, tu as raison :we: Qu'est ce que je me complique la vie ! ...

[raito123]

Bah oui Busard, tu as raison :we: Qu'est ce que je me complique la vie ! ...

Et tu peux simplifier ta vie et nous montrer la démarche?

[tize]

Et tu peux simplifier ta vie et nous montrer la démarche?

Bonjour Raito123,
Je ne comprends pas ? Montrer quelle démarche ? Busard_des_Roseaux a déjà tout fait...ou tu veux encore plus de détail ?

[raito123]

Salut, tize
il n'y a pas une autre méthode sans dévelpement limité?

[tize]

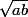
Ah d'accord...bah je ne sais pas trop, un truc comme ce que j'avais tenté de faire dans mon message #6 ? Le problème c'est qu'il faut majorer par un truc qui tend vers et là je ne vois pas trop...je vais voir si je trouve une idée mais c'est pas gagné... :we:

[raito123]

okey merci tize
Il va falloir trouver une fonction je pense.

[shyne99]

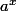
J'ai un souci avec la solution proposée, je ne comprend pas du tout le devellopement de , si c'est un devellopement limitée notre prof nous a interdit de l'utiliser ( car ça nous désaventager par rapport au turbo ),

j'ai encore cherchée ce matin mais impossible de la faire cette "bip" de limite.

[tize]

Dans ce cas tu peux minorer comme je l'ai fait dans mon post #6 puis pour la majoration :
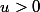
Pour et comme on avait déjà la minoration avec la concavité du ln, on a donc égalité...

[Culioli]

De mon temps, on jetais un œil dans le Polya-Szego (Inequalities).
Ce n'est jamais du temps perdu.
L'exercice proposé ici doit être dans les premières pages.

[tize]

De mon temps, on jetais un œil dans le Polya-Szego (Inequalities).
Ce n'est jamais du temps perdu.
L'exercice proposé ici doit être dans les premières pages.

Salut Culioli :we: ,
oui sans doute...mais je ne l'ai pas sous la main alors...mais c'est sur que c'est bien pratique, les inégalités ça peut être vraiment horrible...

[shyne99]

Je pense qu'il doit y avoir une methode sans utiliser le theoreme des gendarmes, en simplifiant l'expression parce qu'on a jamais utiliser de tel methode en TD , j'essaye , j'essaye mais j'y arrive pas et ça me gave, bref si quelqu'un a une methode par le calcule elle serait la bienvenue. Bon j'y retourne...


Merci d'avance les gars.

[shyne99]

Dsl pour le double post mais j'ai réussi simplement par le calcul, voila comment on fait ,

on compose par le ln ça donne : = = la dérivée en 0 de

soit :
en reprenant l'exponnentielle on a bien :