Probleme de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 30 Jan 2006, 18:15
par Anonyme » 30 Jan 2006, 18:15
Quelle est la limite de
=\frac{1}{2}\left(-x+\left(\frac{x^2}{2\pi}\right)\right)cotan \left( \frac{x}{2} \right))
quand x tend vers 0.f etant de fini sur 0,pi.
merci
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 30 Jan 2006, 18:22
par Chimerade » 30 Jan 2006, 18:22
C'est -1 il me semble
-
Anonyme
 par Anonyme » 30 Jan 2006, 18:27
par Anonyme » 30 Jan 2006, 18:27
en ecivant la fonction,tu as fais une erreur le 2pi est au denominateur.
-
leibniz
- Membre Relatif
- Messages: 407
- Enregistré le: 30 Mai 2005, 10:00
-
 par leibniz » 30 Jan 2006, 18:28
par leibniz » 30 Jan 2006, 18:28
Ok c'est reglé, mais M. Chimerade a répondu avant la modification.
A+
-
Anonyme
 par Anonyme » 30 Jan 2006, 18:32
par Anonyme » 30 Jan 2006, 18:32
OK
pourquoi c'est-1?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 30 Jan 2006, 19:54
par abcd22 » 30 Jan 2006, 19:54
On fait un développement généralisé de cotan en 0 :
})
tend vers 1 en 0, on peut en faire un développement limité, et on en déduit que
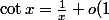)
au voisimage de 0, d'où la limite.
-
Anonyme
 par Anonyme » 30 Jan 2006, 20:12
par Anonyme » 30 Jan 2006, 20:12
Tu peux me faire svp le detail du devellopement limite car j'arrive pas a comprendre.
-
Anonyme
 par Anonyme » 30 Jan 2006, 20:25
par Anonyme » 30 Jan 2006, 20:25
la limite etant -1 ou 0.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 30 Jan 2006, 20:29
par abcd22 » 30 Jan 2006, 20:29
En fait ici on a juste besoin de la limite de x cotan x en 0, donc c'est pas vraiment la peine de faire un développement généralisé (avec un quotient, puis un produit...) Par définition de la limite, au voisinage de 0,
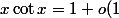)
, donc
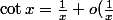)
(le résultat est moins précis que celui que j'ai donné dans mon post précédent mais il suffit). On remplace dans l'expression de f :
 = \frac{1}{2}\left( -x +\frac{x^2}{2\pi} \right)\left( \frac{2}{x} + o(\frac{1}{x}) \right) = \frac{1}{2}\left( -1 +\frac{x}{2\pi} \right)\left( 2 + o(1) \right) = -1 + o(1))
(le x/2Pi rentre dans le o(1)), donc la limite en 0 est -1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
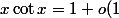) , donc
, donc 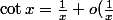) (le résultat est moins précis que celui que j'ai donné dans mon post précédent mais il suffit). On remplace dans l'expression de f :
(le résultat est moins précis que celui que j'ai donné dans mon post précédent mais il suffit). On remplace dans l'expression de f : = \frac{1}{2}\left( -x +\frac{x^2}{2\pi} \right)\left( \frac{2}{x} + o(\frac{1}{x}) \right) = \frac{1}{2}\left( -1 +\frac{x}{2\pi} \right)\left( 2 + o(1) \right) = -1 + o(1)) (le x/2Pi rentre dans le o(1)), donc la limite en 0 est -1.
(le x/2Pi rentre dans le o(1)), donc la limite en 0 est -1.