Problème fonction Arcsin
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
par Dlzlogic » 02 Déc 2012, 12:30
Bonjour,
La formule ???=2t/(1+t²) ne vous dit rien ?
Si j'étais vous, je commencerais par chercher dans cette direction.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 12:34
2t/(1+t²) = 2t(Arctan t) il me semble mais l'exercice est :
"simplifier par dérivation chacune des expressions suivant"
mais je vais chercher du coté que vous me proposez ! merci
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:35
ThekamikazeFou a écrit:Bonjours, j'ai un exercice que je trouve très bizarre.
j'ai une fonction
= Arcsin(\frac{2X}{1+x^2}))
je dois la dérivée puis l'intégré pour normalement retrouver une forme plus simple de la fonction.
Or c'est loin d'être le cas !!
la fonction est définis sur R et sa dérivée aussi.
la dérivé de la fonction est
^2)}}{sqrt{\frac{x^2-2x+1}{1+X^2}}})
Il faut simplifier l'expression de la dérivée : par exemple
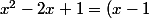^2)
, etc.
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:36
Dlzlogic a écrit:Bonjour,
La formule ???=2t/(1+t²) ne vous dit rien ?
Si j'étais vous, je commencerais par chercher dans cette direction.
à quoi cela peut-il servir dans cet exo ???
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:37
ThekamikazeFou a écrit:2t/(1+t²) = 2t(Arctan t) il me semble
non ce n'est pas ça.
Et je pense que ce n'est pas la peine de suivre les "conseils" de Dlzlogic...
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:41
ThekamikazeFou a écrit:j'ai une fonction
la dérivé de la fonction est
je pense aussi qu'il y a une erreur dans le calcul de la dérivée !
Dérivée de arcsin(u(x)) = ?
-
Defiance
- Messages: 6
- Enregistré le: 06 Sep 2012, 17:56
-
par Defiance » 02 Déc 2012, 12:42
Pourquoi ne pas essayer un changement de variable ? en posant t=tan x/2 on a sin x = 2t/1+t² (c'est les formules utilisant la tangente de l'angle moitié)
Ca va te permettre de beaucoup simplifier !
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:44
Defiance a écrit:Pourquoi ne pas essayer un changement de variable ?
sauf si l'exo est "dériver, simplifier, intégrer".
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 12:46
oui en effet ce n'est pas ça je suis bête...
d(Arctan x) = 1/(1+x²)
leon1789, j'ai essayé de factorisé, simplifier etc, mais je reste bloqué à ceci :
 = \frac{-2x^2+1}{(1+x^2)^2}*\frac{sqrt(1+x^2)}{|x-1|})
en effet c'est dériver, simplifier, intégrer...
si je suis vraiment bloqué je ferais un changement de variable.
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:49
ThekamikazeFou a écrit:leon1789, j'ai essayé de factorisé, simplifier etc, mais je reste bloqué à ceci :
en effet c'est dérivée, simplifié, intégré...
Il faut commencer par calculer la dérivée correctement...
dérivée de arcsin(u(x)) = ?
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:49
ThekamikazeFou a écrit:si je suis vraiment bloqué je ferais un changement de variable.
tout dépend des consignes pour l'exo...
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 12:59
Il vaut mieux rendre l'exo fait en suivant les consignes :lol3:
Ok pour ta dérivée.
Now, factorise
^2)})
et
)
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 13:13
leon1789 a écrit:Il vaut mieux rendre l'exo fait en suivant les consignes :lol3:
je ne peux pas dire le contraire !
alors pour
^2}{1+x^2})
et
(-x+1)}{(1+x^2)^2})
j'ai donc
 =\frac{2(x+1)(-x+1)}{(1+x^2)^2}*\frac{|1+x^2|}{(x-1)^2})
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 14:10
oups oui en effet j'avais oublié de mettre u au carré ...
donc voilà ou j'en suis :
^2} = \frac{(x-1)^2(x+1)^2}{(1+x^2)^2})
et donc
 = \frac{2(x+1)(-x+1)}{(1+x^2)^2} * \frac{|1+x^2|}{|x-1||x+1|})
??
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 16:23
Je remonte le sujet, je suis bloqué, et c'est à rendre pour demain :/
quelqu'un pour m'aider?
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 02 Déc 2012, 18:00
ThekamikazeFou a écrit:oups oui en effet j'avais oublié de mettre u au carré ...
donc voilà ou j'en suis :
et donc
??
ok
disons que
se simplifie sans |.|
regarde les facteurs
)
qui s'éliminent
et enfin
et
se simplifient aussi
Bref, il reste quoi sur quels intervalles ?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
par ThekamikazeFou » 02 Déc 2012, 21:23
Oui enfait j'etais simplement bloqué a cause des valeur absolue...
J'ai finalement 2/(1+x^2) qui est egale en integrant a 2Arctanx
Merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
