Problème de la fermeture

[busard_des_roseaux]

bonjour,

je vous fait part du problème classique suivant:

description géométrique:

soit un cercle , délimitant le disque ouvert
Inclu dans , un cercle

Par un point de , on mène une tangente à
qui recoupe le cercle en un point

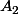
On itére le procédé à partir du point

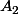
A quelles conditions obtient on une ligne polygonale ...
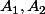
qui se referme au bout d'un nombre fini d'étapes ?

Quid si l'on remplace et/ou par une ellipse ?
et/ou par des arcs fermés délimitant
un convexe ?

[BQss]

Il me semble que c'est une suite qui dépend du rapport des rayons r1 et r2 . Quand r1 sur r2 tend vers 1 le nombre de cotés du polygone tend vers l'infini.

Voila apres le plus dur c'est de se pencher sur les termes de la suite et sur la condition d'arrêt ;), fonction du rapport des rayons :briques: . J'ai pas trop le temps "d'investiguer" j'suis au taf :P, en tout cas sympa ton probleme busard.

[The Void]

Je trouve que la ligne se referme ssi il existe k,n entiers tels que

J'ai juste?