Probleme exo sur equation différentielle avec séries

[benj3850]

salut a tous,

j'ai un petit probleme sur une resolution d'équation différentielle avec les séries :

soit (E) : x^2*y''+4xy'+(2-x^2)*y-2=0

on cherche y sous forme de série entière c'est à dire :

somme de n=o à +oo de An*x^n


le problème c'est que j'arrive à faire ce type d'exercice s'il y aurait juste : x^2*y''+4xy'+(2-x^2)*y = 0 mais là avec le -2 ca me bloque :hein:

merci d'avance pour vos réponses

[yos]

Bonsoir.
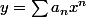
Je ne vois pas en quoi le -2 complique les choses. En posant , le premier membre de l'équadiff aura pour terme constant , et donc .

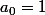
[benj3850]

désolé je ne comprend pas car moi je developpe tout et je met ensuite tout en facteur de x^n mais il y a le -2 après, en dehors de la somme...

[yos]

,
.
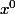
Ensuite tu écrit que la série entière du premier membre est nul, donc tous ses coefs sont nuls. Mais les coefs de et de sont à regarder "à part" car certaines sommes commencent à 0, d'autres à 1, et d'autres à 2.
Ainsi le coef constant est donc .
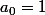
Le coef de x est , donc .
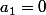
Et pour , tu as , donc .

[benj3850]

ah dacor ok, je voyais pas ca comme ca :we: . Merci beaucoup de ton aide yos

[yos]

Je penche pour chx/x² mais faut vérifier.

[benj3850]

pour an j'ai trouvé : a(2n)=2/(2n+2)! car les termes impairs sont nuls
je ne sais pas si tu a trouvé pareil

[benj3850]

d'ailleur une fois trouvé a(2n), faut faire quoi ? lol, car ca me donne alors :

somme de 0 à +oo de (2x^2n)/(2n+2)!

il y a aussi le question : montrer qu'il y a au plus une série entière dont la somme soit solution de cette equation sur l'intervalle de convergence

[yos]

On reconnait le DSE de 2(chx-1)/x² non?
Pour l'unicité, c'est évident car on a raisonné par condition nécessaire.

[benj3850]

ah ouai exact ;)
merki :)

[yos]

tention j'ai modifié.