Problème d'équation différentielle

[camille75]

bonjour,

*Je dois résoudre l'équation homogène de E sur les intervalles ]-oo,0[; ]0,4[ ; et ]4,+oo[

(E): x(4-x)y'+(2-x)y=1

Je l'ai résolue sur ]0,4[ mais sur les deux autres intervalles j'ai des problèmes de définition

sur ]0,4[ je trouve y=C/(racine(x(4-x))
avec C constante

Je ne vois pas comment résoudre l'équation différentielle sur ]-oo,0[ et sur ]4,+oo[ sachant qu'on a quelque chose qui n'est pas défini

j'obtiens:
y'/y=-(2-x)/(x(4-x)) et ça c négatif donc on ne peut pas passer au ln car

-(2-x)/(x(4-x)) on peut l'intégrer en -(1/2)*ln(x(4-x))

vous êtes d'accord ou pas ???

* Je dois également montrer que (Pi)/2-arcsin(u) est équivalent à racine(1-u²) quand u tend vers 1 on me propose de calculer sin(Pi/2-acsin(u))

Merci =)

[fourize]

:zen: ATTENTION :zen:

ce sujet est en doublon avec celui qui porte ce titre:
equation différentielle et equivalent

merci aux Veilleur de rectifier ce problème !

[mathelot]

aloha,

quelques infos:

i)
une primitive de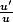 est
cette formule est plus générale et marche si u prend des valeurs négatives

ii)
deux primitives d'une même dérivée, égales en un point, restent égales sur un intervalle mais pas nécéssairement sur un domaine de définition
qui est la réunion disjointe de plusieurs intervalles

pratiquement, ça te fait une constante (générique) K par intervalle.

iii)
une égalité de la forme

donne, en considérant l'exponentielle

soient deux courbes intégrales, les fonctions solution étant continues.