Problème distinction cas réel cas complexe équations differe

[Mart55]

Bonjour à tous !

Je viens sur ce forum car j'ai une question pour le chapitre des équations différentielles.
Voilà, je vois que sur les définitions du cours (équations de second ordre), ils distinguent le cas où on est sur R ou le cas de C. Ce que je comprend pas, c'est la différence que ça fait. Parce que, pour le polynôme caractéristique, si delta est négatif, on se retrouve dans un cas dans C, et si delta est positif ou nul, non. Mais je n'ai pas l'impression que c'est cela qui fait que le cours distingue R et C.

C'est d'autant important pour moi de comprendre que ça fait déjà deux exos ou la correction distingue le cas Réel et le cas complexe.

Ça serait top de pouvoir m'éclairer
Bonne soirée

[XENSECP]

Salut,

Difficile de t'expliquer ton cours si tu n'as "pas l'impression" que c'est ça...

[Ben314]

Salut,
A mon sens, dans un tel chapitre, on fait la distinction entre les deux du fait que :
1) De façon purement mathématiques, c'est quasi systématiquement plus simple de résoudre l'équation dans C (du fait que l'équation du second degrés qu'on a à résoudre a systématiquement des solutions dans C et pas forcément dans R).
2) Les équation différentielles, ça sert dans des tonnes de branches autres que les maths (dans des tas de branches de la physique et dans des tonnes d'autres domaines) et que dans ces cas "concrets", quasi systématiquement, on cherche les solutions réelles de l'équation différentielle (il est assez rare que la vitesse d'une bagnole soit égale à V=(3+2i) Km/h...)

Donc, pour une même équation différentielle, il faut savoir donner l'ensemble des solutions complexe (i.e. des fonctions de R->C) de l'équation, mais il faut aussi savoir donner l'ensemble des solutions réelles (i.e. des fonctions de R->R) de l'équation.
Dans la "théorie théorique", ça ne fait pas une énorme différence, modulo d'avoir parfaitement compris comment fonctionnent les exponentielles complexes. Sauf qu'assez souvent les étudiants n'ont pas une "grande dextérité" (sic...) concernant ce passage, donc on se fend, y compris en cours, de donner les deux ensembles de solutions.

[Mart55]

Bonjour,

Merci pour la réponse. Donc, si je comprend bien, si j'ai un delta supérieur à 0 (je parle d'équations du second ordre), je n'aurai pas à distinguer. Cependant, si delta est inférieur à 0, il y a des solutions complexes (avec sinus, cosinus) ET des solutions dans R ?

[Ben314]

Oui, c'est (à peu prés) ça.
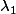
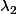
En fait, si on veut un peu rentrer dans les détails, dans le cas d'une équa-diff homogène (du second degré à coefficients réels constants) si ton polynôme caractéristique a un discriminant strictement positif, il va avoir deux racines réelles et et :
- Les solutions complexes seront les fonction de la forme où et sont deux constantes complexes arbitraires.
- Les solutions réelles seront les fonction de la forme où et sont deux constantes réelles arbitraires.
Donc dans ce cas là, on se dit que c'est pas la mer à boire de passer des solutions réelles aux solutions complexes...

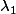
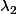
Mais par contre, si le discriminant est strictement négatif, alors le polynôme caractéristique va avoir des racines complexes (conjuguées) et (mais pas de racines réelles) et :
- Les solutions complexes seront les fonction de la forme où et sont deux constantes complexes arbitraires.
(donc pour le cas complexe, c'est exactement la même chose que lorsque le discriminant était >0 et c'est normal vu que dans C, dans les deux cas, le polynôme admet deux racines).
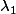
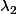
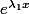
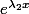
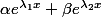
Par contre, pour le cas réel, ça change pas mal de truc : on serait évidement tenté d'écrire que les solutions réelles, c'est la même chose où on prend les constantes et réelles, mais ça ne marche pas du tout car, vu que et ne sont pas réel, et ne le sont sans doute pas non plus donc ce n'est pas en prenant et réels qu'on va obtenir que est réel.
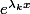
Il faut donc regarder de plus près les parties réelles et imaginaires des deux en revenant à la définition de ce qu'est l'exponentielle d'un nombre complexe.
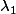
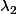
Et après quelques lignes de calcul, on fini par trouver que, dans ce cas, les solution réelles de l'équation sont les fonctions de la forme où et sont la partie réelle et imaginaire de (ou de , mais ça revient au même vu qu'ils sont conjugués) et où et sont des constantes réelles arbitraires.
Formule qu'on peut aussi (via quelques formules de trigo) réécrire sous la forme où et sont deux constantes réelles arbitraires.

[mathelot]

Dans le cas d'équations linéaires sans second membre, l'ensemble des solutions est un espace vectoriel
sur de dimension n, disons. C'est un espace vectoriel sur de dimension 2n.
Quand les coefficients de l'équation sont réels, en considérant des combinaisons linéaires
des solutions complexes et de leur conjuguées, on peut obtenir une base réelle du R-espace vectoriel

[Ben314]

@mathelot : je trouve que ta façon d'écrire le truc prête un peu (voire pas mal) à confusion :
L'ensemble des solutions complexes de l'équation est effectivement un espace vectoriel sur C qui est de dimension n (sur C).
Bien sûr, ce même espace vectoriel (i.e. l'ensemble des solutions complexes de l'équation) peut être vu comme un espace vectoriel sur R qui va être de dimension 2n (sur R).
Mais c'est quand même très rare qu'on ait besoin de ce point de vue (l'ensemble des solutions complexes vue comme espace vectoriel réel) alors que ce qu'on manipule bien plus fréquemment, c'est l'ensemble des solutions réelles de l'équation vue comme espace vectoriel réel.
Et là, de nouveau, la dimension est égale à n et pas à 2n.

Enfin, bref, pour voir l'ensemble des solutions comme un e.v. de dimension 2n, il faut quand même un peu "loucher" (i.e. l'œil droit et l'œil gauche ne vont pas tout à fait dans la même direction, l'un regarde "réel" et l'autre "complexe"...)

[mathelot]

si on considère l'équation

on a deux solutions dans :
et
si on tire il faut bien diviser par le scalaire 2i
ce qui se fait dans un C-espace vectoriel ?

[Mart55]

Merci pour les explications,
Tout devient plus clair maintenant !! Il me reste plus qu'à bien étudier les démonstrations.

Dernière petite question qui n'est pas vraiment lié: Est ce qu'on peut dire que la solution de y" - y = 0 est soit:
1) A exp(x) + B exp(-x)
2) C ch(x) + K sh(x) (quitte à changer les constantes)

Je suppose que oui mais je voulais confirmer pour être sur d'être bon dans mon exercice
Ma solution finale étant: A*(e(x) + e(-x)) + e(-x)
Celle de l'exercice: C*ch(x) - sh(x)

(Je garde les mêmes A,B, C et K que dans mes1) et 2) )

Bonne soirée

P.S: Je n'ai pas fais les espaces vectoriels encore!!

[Ben314]

1) A exp(x) + B exp(-x)
2) C ch(x) + K sh(x) (quitte à changer les constantes)

Oui, c'est bien la même chose.
Par contre, si tu n'as pas vu la notion d'espaces vectoriels (voir d'espaces affine vu qu'en l'occurrence c'est de ça qu'il s'agit), c'est un peu chiant à démontrer : tu est plus ou moins obligé de vérifier que tout ce qu'on peut écrire sous la forme 1) peut aussi s'écrire sous la forme 2 et réciproquement.

Dans le sens 2) => 1), c'est assez immédiat vu les définitions de Ch(x) et Sh(x) :
C.Ch(x)+K.Sh(x) = C.(e^x+e^-x)/2+K.(e^x-e^-x)/2 = (C+K)/2.e^x+(C-K)/2.e^-x
qui est bien de la forme 1 (avec A=(C+K)/2 et B=(C-K)/2 )

Dans l'autre sens, on peut suivre la même démarche une fois qu'on a constaté que exp(x)=Ch(x)+Sh(x) et que exp(-x)=Ch(x)-Sh(x)

[Mart55]

Ok ! J'en conclue que la repons final de l'exercice peut être donnée des deux manières dites dans mon message également !

D'après vos messages, les espaces vectoriels sont tres liés aux équations différentielles j'ai hate d'en savoir +.
Merci pour vos messages !

[Ben314]

D'après vos messages, les espaces vectoriels sont très liés aux équations différentielles j'ai hate d'en savoir +.

Les espaces vectoriels, c'est très lié, on va dire à 75% de ce qu'on fait en mathématique : il n'y a pas beaucoup de branches où on ne les utilise pas du tout.
Dans le lot des domaines où ils sont super utiles, il y a effectivement les équations différentielles, mais c'est loin d'être le seul.

[mathelot]

et sont les parties paire et impaire de