Un problème de Cauchy

[mehdibj]

bonsoir tout le monde , dans un exercice qui consiste a vérifier la forme d'une solution pour une équation de Cauchy assez complexe
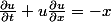
( <-- u=u(x,t)
).
je doit résoudre l'équation différentielle suivante qui me bloque :
<--- dans ce cas u est enfaite û(t) fonction d'une seul variable t
j'ai totalement oublier comment résoudre se genre d'équation quelq'un peut m'aider , Merci d'avence

[mathelot]

Bônsoir,
u du =-x dx
En intégrant
(1/2)u^2 = - (1/2)x^2+C
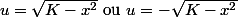
où K est une constante d'intégration