Problème de cartes - urgent

[dalex160]

Bonjour,

Je suis en école d'ingénieur et n'est donc qu'un vague reste de mathématique concernant les probabilités. Mon problème est assez complexe et c'est pourquoi je vous remercie par avance de l'aide que vous m'apporterez.

Je m'explique: Je cherche à réaliser un programme informatique (sous MATLAB) qui rendrait compte des possibilités d'un mélange de carte à l'américaine ( mélange qui consiste à séparer un paquet en deux parties pas forcément égales puis à intercaller une ou plusieurs cartes d'un des paquets entre les cartes du second paquet).

Pour cela, j'ai un paquet constitué de N cartes. Ma question est la suivante, en supposant que je coupe mon paquet à la place k, je me retrouve avec deux paquets : un de k cartes, l'autre de N-k cartes. Combien de possibilités de mélange différentes je peux obtenir sachant qu'entre chaque carte du second paquet je peux intercaller AU HASARD un nombre compris entre 1 et k cartes du premeir paquet. Au début je pensais simplement à N! possibilités mais la littérature est contre moi.. je suis vraiment désespéré et je serai vraiment sauvé si quelqu'un pouvait m'aider.

Mon but ultime c'est donc de savoir COMBIEN de possibilité de mélange à l'américaine existe-t'il pour un paquet de N cartes.

J'espere que mon problème est clair. Si jamais vous ne comprenez pas demandez moi!

Merci beaucoup

[dudumath]

cela revient à intercaler n-k cartes entre k cartes, autrement dit a calculer le cardinal de l'ensemble des solutions de



Plus généralement, tu peux chercher l'ensemble des n-uplets vérifiant:



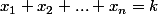
Des pistes...

en notant C(k,n) le cardinal des solutions, peux tu déterminer C(0,n), C(1,n),
C(2,n) (en fonction de n) et C(k+1,n) en fonction de k, puis déterminer G(k+1,n+1) en fonction de G(k,n+1) et G(k+1,n)
et en déduire que G(k,n) = ... k parmi (n+k-1)

[Finrod]

je peux obtenir sachant qu'entre chaque carte du second paquet je peux intercaler AU HASARD un nombre compris entre 1 et k cartes du premier paquet

les deux paquets jouent des rôle symétriques si tu intercales entre 0 et k cartes du premier chaque fois.

Il me semble que dudu traite ce cas symétrique là. Le "1" est il important ou est ce un accident ?

@dudu : C'est machiavélique, la réponse à la fin.

[alavacommejetepousse]

bonjour

peux tu un peu préciser

on intercale vraiment au minimum 1 carte pas plutôt 0?

dudumath cela ne va pas car tu ne tiens pas compte de la valeur de la carte seulement du nombre intercalé

[dalex160]

Bonjour,

Tout d'abord merci de vous être penché sur mon problème, je ne savais vraiment quoi faire.
Je savais bien que j'aurai du mal à expliquer mon problème! Voici une vidéo de ce qu'est le mélange américain (elle dure 20 secondes):http://www.youtube.com/watch?v=fzqDpkwbEUI&feature=related

Ma question est donc la suivante : combien de mélange différents possibles (en fonction de N le nombre de cartes) peut on effectuer ?
Ce nombre doit forcément dépendre du nombre de coupe possible (ça c'est N ou N-1 je pense) et aussi du nombre x de cartes qui s'intercalent toutes les y cartes du second paquet (où x et y varient sans cesse).

@dudu: j'ai essayé ta méthode. Le problème c'est que la personne qui m'évalue (celle qui m'a posé le problème et à qui je ne peux pas demander la réponse) m'a dit que pour N=14, il trouvait approximativement 69 000 possibilités!! ce qui ne concorde pas avec ce que je trouve pour ta méthode..

J'espere que je me suis bien expliqué..

Merci encore!

[dudumath]

dudumath cela ne va pas car tu ne tiens pas compte de la valeur de la carte seulement du nombre intercalé

Je pensais que le jeu de cartes était "fixé" mais du coup rien ne le disait donc j'ai inventé ça^^, donc forcément ça va plus!