Problème calcul de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:01
par zelda007 » 11 Mar 2008, 19:01
Salut,
J'ai encore une limite à calculer avec partie entière : x * E(1/x) en + l'infini.
Malheureusement, en utilisant la définition de la partie entière, les encadrements ne donne aucun résulat.
Une idée ?
Merci
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mar 2008, 19:06
par Skullkid » 11 Mar 2008, 19:06
Bonsoir, il me semble pourtant que ça marche, utilise x-1 <= E(x) <= x.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:12
par zelda007 » 11 Mar 2008, 19:12
C'est normal je me suis trompé dans l'enoncé ! lol
Correction faite :we:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mar 2008, 19:16
par Skullkid » 11 Mar 2008, 19:16
Ah, oui en effet. ^^
Alors, est-ce que tu as une idée de ce que peut devenir E(1/x) quand x devient très grand ?
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:20
par zelda007 » 11 Mar 2008, 19:20
Ca tends vers 0 non ? Mais on a une forme indéterminée...
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mar 2008, 19:25
par Skullkid » 11 Mar 2008, 19:25
Ça tend vers 0 oui, mais ça fait mieux que ça ! Que vaut E(x) quand x est strictement compris entre 0 et 1 ?
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:31
par zelda007 » 11 Mar 2008, 19:31
Ca vaut 0 mais en quoi ca apporte quelque chose ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mar 2008, 19:33
par Skullkid » 11 Mar 2008, 19:33
Quand x est strictement supérieur à 1, 1/x est strictement compris entre 0 et 1, donc E(1/x) = 0. A fortiori x*E(1/x) = 0.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:40
par zelda007 » 11 Mar 2008, 19:40
Oui mais "0x0" n'est pas une forme indéterminée ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mar 2008, 19:46
par Skullkid » 11 Mar 2008, 19:46
0x0 ça fait 0 ^^
C'est
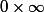
qui est indéterminée. Ça signifie qu'a priori quand on multiplie quelque chose de très grand par quelque chose de très petit, on peut pas savoir ce que ça va donner. Mais ici E(1/x) n'est pas simplement "petit", il est rigoureusement égal à 0 (à partir d'un certain moment). x aura beau être aussi grand qu'il veut, un nombre multiplié par zéro ça fait toujours zéro.
-
Magemax
- Messages: 4
- Enregistré le: 11 Mar 2008, 18:30
-
 par Magemax » 11 Mar 2008, 19:47
par Magemax » 11 Mar 2008, 19:47
Mmmh par "forme indéterminée" il ne faut pas comprendre "c'est pas possible de connaître la limite", mais "il faut la chercher un peu plus loin". Ici, il ne faut pas aller bien loin :
Dans ce cas, E(1/x) vaut carrément 0 à partir de 1.
Donc x*E(1/x) vaut également 0 pour tout x appartenant à [1;+l'infini[
Autant dire que ta fonction tend vraiment vers 0.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 11 Mar 2008, 19:49
par zelda007 » 11 Mar 2008, 19:49
Oui effectivement, donc je vais aller dormir :we: :we:
Merci
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 11 Mar 2008, 21:00
par ffpower » 11 Mar 2008, 21:00
t un couche tot toi...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
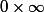 qui est indéterminée. Ça signifie qu'a priori quand on multiplie quelque chose de très grand par quelque chose de très petit, on peut pas savoir ce que ça va donner. Mais ici E(1/x) n'est pas simplement "petit", il est rigoureusement égal à 0 (à partir d'un certain moment). x aura beau être aussi grand qu'il veut, un nombre multiplié par zéro ça fait toujours zéro.
qui est indéterminée. Ça signifie qu'a priori quand on multiplie quelque chose de très grand par quelque chose de très petit, on peut pas savoir ce que ça va donner. Mais ici E(1/x) n'est pas simplement "petit", il est rigoureusement égal à 0 (à partir d'un certain moment). x aura beau être aussi grand qu'il veut, un nombre multiplié par zéro ça fait toujours zéro.