Problème de boîte

[kenso]

Bonjour !


Voilà, j'ai un petit soucis avec l'exercice suivant :

On veut construire une boîte en bois carrée de côté a, ayant un volume V=108 cm3. La boîte n'a pas de couvercle, quelles dimensions doit-on donner à la boîte pour que le minimum de surface de bois soit utilisée pour la construire ?

Moi j'ai trouvé un h = 6,9 cm et un a = 4 cm (environ), seulement je n'ai pas utilisé l'information concernant la surface, donnée dans l'énoncé.

Donc si quelqu'un pouvait me mettre sur la voie ce serait sympa :happy2:

Il me semble qu'il faut utiliser une dérivée partielle... V (a, h), mais je n'en suis pas certain.


Merci d'avance.

kenso.

[L.A.]

Bonjour.

La boite est à base carrée de coté a, mais à priori non cubique, c'est ça ?
si on note h la hauteur, la surface sans couvercle vaut :
S(a,h) = a² + 4ah
et son volume est V = 108 = a²h
la condition sur le volume implique une relation entre a et h, donc la surface d'une telle boite S(a) ne dépend en fait que de a. Pour moi pas de dérivée partielle donc.

[mathelot]

Bonjour,


je plussoie sur ce qu'écrit L.A,





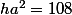
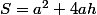
on se ramène à un problème à une seule variable
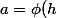puisque l'on peut substituer ou
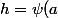dans la seconde égalité.

[kenso]

Slt,

Merci pour vos réponses.

J'avais déjà écris l'équation de S et V, seulement, on se retrouve avec 2 équations et 3 inconnues... ? Il ne me semble pas qu'il y ait une équation qui relie S à V et qui aurait pu compléter le système...


EDIT : Ah, si ! Peut-être : 2 x la dérivée du V + a carrée = S.

[L.A.]

En tout il y a deux équations et deux inconnues :
inconnues : a et h (les dimensions)
équations : V = 108 et S minimal.

Le problème serait à priori que ces équations ne sont pas linéaires, mais si on trouve plusieurs solutions pour a, c'est qu'il y a plusieurs configurations possibles.

[kenso]

Ok, mais là je ne vois pas comment je pourrais arriver à une valeur de a et h chiffrée, vu que je ne connais pas S minimale... ?

P.S : faîtes pas attention au EDIT de mon dernier message. :marteau:

[mathelot]

re,

[L.A.]

Pour minimiser une fonction d'une variable réele S(a), on peut commencer par chercher les zéros de sa dérivée.

Edit : voilà c'est fait. Resterait alors à prouver qu'on est bien face à un minimum global.

[phryte]

je pourrais arriver à une valeur de a et h

Tu dérives S=(a^3+432)/a !

[kenso]

Ok !

Désolé c'était évident, ça aurait du me sauter aux yeux :happy2:.

En tout cas merci beaucoup pour votre aide, et la rapidité avec laquelle vous avez répondu ! :++:

Si j'ai des soucis j'hésiterai pas, ce forum est vraiment bien.