Re: Problème avec les équivalents
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
raviel181
- Messages: 5
- Enregistré le: 11 Mai 2018, 19:27
-
 par raviel181 » 11 Mai 2018, 19:35
par raviel181 » 11 Mai 2018, 19:35
Bonjour,
j'ai besoin d'aide à propos des équivalents d'une fonction, je n'ai pas vraiment compris comment on peut le trouver avec les équivalents usuels.
J'ai l'exercice de déterminer un équivalents en 0 de ln(1+x)sin^2(x)
J'ai compris que ln(1+x) est équivalent à x
et sin^2(x) équivalent à x^2
Mais après je ne sais pas comment on fait pour trouver l'équivalent de la fonction.
Et aussi pourquoi les équivalents ne s'additionne pas?
Merci de votre aide


-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 11 Mai 2018, 20:41
par capitaine nuggets » 11 Mai 2018, 20:41
Salut !
Il n'y a pas de problèmes avec les produits :
Si
 \sim x)
et
 \sim x^2)
alors
\sin^2(x) \sim x \times x^2 = x^3)
.
(
au voisinage de 
).
Les seuls opérations où il peut y avoir des problèmes, c'est l'addition et la composition.
Par exemple, l'exemple typique pour l'addition

et

, mais pourtant :
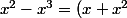+(-x+x^3) \not\sim x +(-x) = 0)
(
tout ça au voisinage de 
).
-
raviel181
- Messages: 5
- Enregistré le: 11 Mai 2018, 19:27
-
 par raviel181 » 11 Mai 2018, 21:21
par raviel181 » 11 Mai 2018, 21:21
merci pour ta réponse
Ah d'accord moi je me suis embrouillé, je croyais qu'on pouvais pas multiplier comme pour les additions
Donc on a juste à trouver les équivalents usuels puis faire la multiplication
Mais du coup pour les additions comment on fais ?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 11 Mai 2018, 21:53
par Pseuda » 11 Mai 2018, 21:53
raviel181 a écrit:Mais du coup pour les additions comment on fais ?
Bonsoir,
On peut utiliser les "o". Par exemple :
 = x + o(x))
)
On en déduit :
 + \sin x = 2x + o(x) \sim 2x)
ou encore :
 = x + o(x))
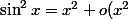)
On en déduit :
 + \sin^2 x = x + x^2 + o(x) + o(x^2) = x + o(x) \sim x)
-
raviel181
- Messages: 5
- Enregistré le: 11 Mai 2018, 19:27
-
 par raviel181 » 11 Mai 2018, 22:55
par raviel181 » 11 Mai 2018, 22:55
ah d'accord avec le o(x) je n'y ai jamais vue, je sais pas si ça passe sur une copie .
avec ta méthode c'est beaucoup plus simple^^
et pour un changement de variable c'est pareil ?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 12 Mai 2018, 07:57
par pascal16 » 12 Mai 2018, 07:57
l'équivalent est le premier pas vers le développement limité : DL.
la notation "o" est celle qui permet de bien faire les choses.
par exemple, xsin x à l'ordre 2 en 0.
sinx = x +o(x²)
x*sinx = x²+ xo(x²)
x*sinx = x²+ o(x³)
on a directement un DL à l'ordre 3 avec seulement un développement sin(x)=x... qu'on pourrait croire à l'ordre 1, mais on le sait car on a gardé le "petit o".
Inversement, en multipliant par 1/x, ou en divisant par un polynôme, on perd de la précision.
cox(x), paire, permet de gagner un ordre, avec 1-x²/2+o(x³) , on se dit qu'on va tomber sur de l'ordre 3
(cosx-1)/x
= (1-x²/2+o(x³) -1 )/x
= (x²/2+o(x³) )/x
= x/2 + o(x²)
on a perdu un degré; mais on sait qu'on a du DL à l'ordre 2.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Mai 2018, 09:46
par Pseuda » 12 Mai 2018, 09:46
raviel181 a écrit:ah d'accord avec le o(x) je n'y ai jamais vue, je sais pas si ça passe sur une copie .
avec ta méthode c'est beaucoup plus simple^^
et pour un changement de variable c'est pareil ?
Bonjour,
Cette écriture avec les "o" est rigoureuse. C'est évidemment bon sur une copie si c'est bien justifié.
On utilise :
)
pour passer de l'un à l'autre.
On peut utiliser les o pour le changement de variable (DL des fonctions composées).
-
raviel181
- Messages: 5
- Enregistré le: 11 Mai 2018, 19:27
-
 par raviel181 » 12 Mai 2018, 16:01
par raviel181 » 12 Mai 2018, 16:01
ah d'accord après je n'ai pas vue les DL ça doit être pour ça que je n'ai pas appris o(x)
en tout cas merci beaucoup vous m'avez beaucoup aidé

-
raviel181
- Messages: 5
- Enregistré le: 11 Mai 2018, 19:27
-
 par raviel181 » 13 Mai 2018, 16:44
par raviel181 » 13 Mai 2018, 16:44
bonjour désolé de vous ré-embêter mais voilà j'ai une limite à déterminer
(e^(x-1)-1)/ln(x) en 1
j'arrive à trouver le résultat avec les équivalents mais je n'arrive pas sans les utilisés
pouvez-vous s'il vous plaît ,m'aider dans ma quête^^
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 13 Mai 2018, 21:54
par Pseuda » 13 Mai 2018, 21:54
Bonsoir,
Sans les utiliser, on peut faire un changement de variables t=x-1, et transformer en ((e^t-1)/t)*(t/ln(t+1)), dont les limites sont connues.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
