Problème avec des intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
par balteo » 28 Juil 2010, 18:48
Bonjour,
J'essaye de résoudre le problème suivant:
***************
Soit l'intégrale suivante définie pour n, entiers positifs:
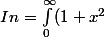^{-n} dx)
En déduire que In=2n(In-In+1)
De là, montrer que
^{-4} dx=\frac{\pi}{32})
***************
J'ai essayé d'intégrer In, sans succès.
Quelqu'un peut-il me donner des pistes pour la résolution de ce problème svp?
Merci,
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 28 Juil 2010, 18:59
Bonjour,
pour obtenir la relation de récurrence, on peut partir de
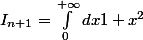^{n+1}} =\int_0^{+\infty}\fr{1+x^2-x^2}{\(1+x^2\)^{n+1}}dx = \int_0^{+\infty}\fr{dx}{\(1+x^2\)^n}-\fr12\int_0^{+\infty}x\fr{2x}{\(1+x^2\)^n}dx)
puis faire une intégration par parties dans la dernière intégrale.
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
par balteo » 28 Juil 2010, 19:39
girdav a écrit:Bonjour,
pour obtenir la relation de récurrence, on peut partir de
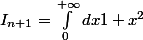^{n+1}} =\int_0^{+\infty}\fr{1+x^2-x^2}{\(1+x^2\)^{n+1}}dx = \int_0^{+\infty}\fr{dx}{\(1+x^2\)^n}-\fr12\int_0^{+\infty}x\fr{2x}{\(1+x^2\)n}dx)
puis faire une intégration par parties dans la dernière intégrale.
Merci Girdav,
Désolé je ne comprends pas dès le début: tu mets
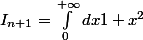^{n+1}})
Remarque le "n+1". Comment se fait-il que ce ne soit pas plutôt "-n+1"? Est-ce une faute de frappe?
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 28 Juil 2010, 19:41
C'est en effet une faute de frappe que j'ai corrigée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
par