Problème d'arithmétique

[mehdibj]

soient des entiers a>1 et n>0 . monter que si 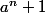est premier alors n est une puissance de 2 .

[Pseuda]

Bonjour,

L'énoncé est incomplet.

[mehdibj]

je viens de le corriger

[Ben314]

Salut,

... si alors n est une puissance de 2 .

Si quelqu'un te dit : Demain, si la météo alors j'irais te voir
Tu comprend quoi toi ?

[mehdibj]

c'est bon j'ai recorrigé l’énoncé

[Pseuda]

Pour commencer, que penses-tu de a^n+1 si n est impair ? Peut-il être premier ?

[Ben314]

- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ? (56=8x7)

[nodgim]

Y a un blocage, là.
Peut être saurais tu donner un facteur de a^n-1 pour commencer ?

[pascal16]

exercice 6 :
http://mp.cpgedupuydelome.fr/pdf/Arithm%C3%A9tique%20-%20Nombres%20premiers.pdf

[mehdibj]

Pour commencer, que penses-tu de a^n+1 si n est impair ? Peut-il être premier ?

je n'arrive pas a comprendre pourquoi pas

[cailloux1]

Bonsoir,

Si est impair, et - est racine du polynôme

[mehdibj]

- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ?
- Peut tu me donner un diviseur "évident" de ? (56=8x7)

aucune idée

[mehdibj]

Bonsoir,

Si est impair, et - est racine du polynôme

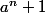
bonsoir,
d'où si n est impaire or je ne dois pas seullement montrée que n est paire mais qu'on peut ecrire

[Pseuda]

Bonsoir,

Si n est impair, alors a^n+1 se factorise en (a+1)*(a^(n-1)-a^(n-2)+a^(n-3)+.... -a+1). Donc a^n+1 n'est pas premier.

Donc si n comporte un facteur impair au moins dans sa décomposition en facteurs premiers, alors a^n+1 n'est pas premier (car n s'écrit ik avec i impair et a^n=(a^k)^i). Pour que a^n+1 soit premier, il faut donc que n soit une puissance de 2.