Probleme algorithme dicothomie maple

[ghassanito]

SALUT ,

Je voudrais bien traduire un algo vers un langage maple , chose que je n'ai pas reussi :/




et voila ma traduction sur maple

[HTML]dichotom:=proc (pre,f,nmax,a,b)
local n,g,d,
n := 1
g:=a
d:=b

while n pre

p:=(g+d)/2;
print(n,d,g,p)
p:=p+1

if f(d)*f(g)>0 then
g:=p
else
d:=p
fi;
od;
end;[/HTML]


En attendant votre aide svp

merci d'avance

[mathelot]

bonjour,
changer la condition
"if f(d)*f(g)>0 then "
en
"if f(p)*f(g)>0 then "

[ghassanito]

salut

après modification et ajout des ";" l'algo est validé mais quand je le teste pour une fonction , sa ne marche pas :/

dichotom:=proc (pre,f,nmax,a,b)
local n,g,d,
n := 1
g:=a
d:=b

while n pre

p:=(g+d)/2;
print(n,d,g,p)
p:=p+1

if f(p)*f(g)>0 then
g:=p
else
d:=p
fi;
od;
end;

[mathelot]

i) remplacer p:=p+1 par n:=n+1.

ii) remplacer "while n<=nmax and (d-b)/2 > pre"
par
"while n<=nmax and (d-g)/2 > pre"

iii)
est ce "do while" plutôt que "while" puisque l'on a un "od" en fin de boucle.

[ghassanito]

salut , bon voila j'ai refait tout l'algo de dichotomie et sa marche maintenant bien , je suis passer à la méthode du point fixe
En passant du psuedo code vers un code maple je me retrouve face a cette erreur
Error, (in pointfixe) cannot determine if this expression is true or false: .1 prec do
m := f(p);
n := n+1;
print(n, p, f(p));
od;
end proc ; [/CODE]


en prenant f:=x->x^2+2*x-4

puis en fesant

h:=pointfixe(f,2,0.1,5)

sa me donne un message d'erreur

[mathelot]

la méthode de Newton calcule des valeurs approchées
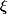
de la racine de l'équation
via


qui converge (dans les bons cas) vers .

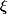
On pose f(x)=x-g(x)

d'où






qui doit converger vers le point fixe (dans les bons cas).