je me rends compte d'une petite coquille de ma part
j'ai écrit
T l N=n = Tn alors que je voulais écrire = T1+T2+...+Tn bien sûr
j'ai modifié,c'est peut être cela qui te bloquait
Probas(traversée de la chaussée par un piéton)
32 messages
- Page 2 sur 2 - 1, 2
Ok!
d'accord!
Merci c'est plus clair pour moi!
si je puis me permettre j'ai encore une question,dans la suite de l'exo j'ai ça:
Montrer que pour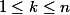
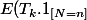=p(1-p)^{n-1} \Bigint_0^t xf(x) dx)
et en fait je vois pas comment m'y prendre?
est-ce encore en rapport avec l'espérance conditionelle??
Si oui,attendez juste un petit peu avant de m'aider... :++:
Merci à vous deux!
d'accord!
Merci c'est plus clair pour moi!
si je puis me permettre j'ai encore une question,dans la suite de l'exo j'ai ça:
Montrer que pour
et en fait je vois pas comment m'y prendre?
est-ce encore en rapport avec l'espérance conditionelle??
Si oui,attendez juste un petit peu avant de m'aider... :++:
Merci à vous deux!
C'est bon,j'ai trouvé!
Dans la suite de l'exercice voici la question ou je bloque...
Pour t>0 no note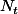 le nombre de voitures pasées au passage clouté avant l'instant t
le nombre de voitures pasées au passage clouté avant l'instant t
Montrer que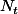 converge presque surement vars
converge presque surement vars 
On pose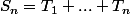
Vérifier que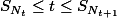
En déduire que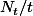 converge presque surement vers
converge presque surement vers ) lorsque t tend vers
lorsque t tend vers 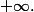
mais là en fait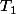 suit une loi exponetielle et en fait
suit une loi exponetielle et en fait =P(T_1+...+T_n\le m))
mais les var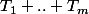 suit la convolée des lois de chaque
suit la convolée des lois de chaque 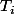 donc a pour densité f convolée m fois de suite.
donc a pour densité f convolée m fois de suite.
Merci d'avance de votre aide! :++:
Dans la suite de l'exercice voici la question ou je bloque...
Pour t>0 no note
Montrer que
On pose
Vérifier que
En déduire que
mais là en fait
mais les var
Merci d'avance de votre aide! :++:
32 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
