Et là je suis vraiment paumé...
Pourriez-vous m'aider svp ?
Probabilités
3 messages
- Page 1 sur 1
Probabilités
par checkmaths » 28 Juin 2017, 20:47
Et là je suis vraiment paumé...
Pourriez-vous m'aider svp ?
Re: Probabilités
par mathsup » 29 Juin 2017, 12:45
Je vous aide un peu mais j'ai la flemme d'aller dans le détail...
D'abord observez que
=E((X_1+...+X_n)(X_1+...+X_n)(X_1+...+X_n)(X_1+...+X_n)))
)
)
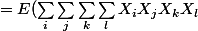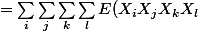(par linéarité de l'espérance)
Il va donc falloir calculer)
. Et là il y a plusieurs cas possibles.
Soit les indices sont distincts donc par indépendance :=E(X_i)E(X_j)E(X_j)E(X_k))
et en calculant l'une de ces espérance vous verrez que ça fait 0.
Soit il y a trois indices différents, donc deux pareils (par exemple i=j) :=E(X_i^2)E(X_j)E(X_k))
et là, ça fera encore 0.
Soit il y a deux indices différents (par exemple i=j et k=l ou bien j=k=l) :=E(X_i^2)E(X_k^2))
et là vous aurez un résultat non nul, ou bien =E(X_i)E(X_j^3))
et ça fera 0.
Soit tous les indices sont les mêmes :=E(X_i^4))
et vous trouverez un résultat non nul.
En faisant un peu de dénombrement et en rassemblant tout ça dans votre somme, vous arriverez à calculer votre espérance.
Pour la question d'après, penser à utiliser l'inégalité de Markov pour majorer la proba avec l'espérance calculée précédemment, puis adapter le
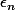
pour que la série obtenue soit convergente. Avec Borell-Cantelli vous pourrez en conclure quelque chose!
D'abord observez que
Il va donc falloir calculer
Soit les indices sont distincts donc par indépendance :
Soit il y a trois indices différents, donc deux pareils (par exemple i=j) :
Soit il y a deux indices différents (par exemple i=j et k=l ou bien j=k=l) :
Soit tous les indices sont les mêmes :
En faisant un peu de dénombrement et en rassemblant tout ça dans votre somme, vous arriverez à calculer votre espérance.
Pour la question d'après, penser à utiliser l'inégalité de Markov pour majorer la proba avec l'espérance calculée précédemment, puis adapter le
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :