Probabilités résolution d'exercice

[Velandco]

Bonjour à tous,
J'ai un léger souci, je n'aime pas du tout les probabilités et j'ai vraiment du mal à résoudre un exercice j'aimerais savoir si quelques uns d'entre vous pourrez m'aider.

Alors voila l'exercice:

On dispose de deux urnes: l'urne U contient une boule blanche et 4 boules noires, l'urne V contient 3 boules blanches et 2 boules noires. Dans l'une des urnes choisies au hasard, on effectue une série de tirage d'une boule avec remise (tous les tirages ont lieu dans la même urne). A cette expérience aléatoire on associe un espace probabilisé que l'on ne cherchera pas à décrire avec plus de précision. Soit Ai l'évènementla ième boule tirée est blanche".
1.Calculer P(A1) et P(A2). A1 et A2 sont ils indépendants?
2.Calculer P(A1 n A2 n ... n An), n appartient à N* (Pour cette question "n" veut dire "inter", il me semble qu'il faut utiliser la formule de probabilité totale)
3.Sachant que les n-1 premiers tirages donnent chacun une boule blanche, quelle est la probabilité d'obtenir une boule blanche supplémentaire au tirage suivant?
4.Sachant que les n premières boules tirées sont blanches, quelle est la probabilité d'avoir tiré dans U? (Pour cette question là il me semble que c'est la formule de Bayes ou la formule des probabilités conditionelle)

Je vous remercie d'avance!

[nuage]

Salut,
pour la question 1 il est presque évident que et 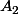ne sont pas indépendants. En effet si on a choisi l'urne V la proba des augmente.
Comme ce que je viens de dire n'est pas très clair, un petit calcul :
Les tirages étant avec remise, il est immédiat que P est constant (cad ne dépend pas de ).
je suppose que





Pour la question 2 on fait comme pour la 1 (c'est, en effet, la formule des probabilités totales)

Pour les questions 3 et 4, comme tu l'as remarqué, la formule de Bayes s'impose.

[Velandco]

Merci beaucoup pour la réponse que tu as envoyé, juste une petite question encore (je suis désolée) mais j'ai du mal à appliquer la formule de Bayes, pourrais tu m'aider stp :help:

[busard_des_roseaux]

j'ai du mal à appliquer la formule de Bayes

la formule de Bayes s'appelle "formule de probabilités des causes"
elle est basée sur le fait que

dans , la proba de B sachant A,
intervient la proba de l'intersection , qui est commutative et qui prête donc à inversion.

on fait donc apparaitre dans la formule.


Ensuite, étant donnée une partition de en une famille finie ,i variant de 1 à n, partition
en évênements qui représente les "causes",

on inverse la proba , ie, la probabilité d'une cause
particulière, l'indice k étatnt fixé, en faisant apparaitre dans la définition de cette proba les où l'indice i varie de 1 à n.

On calcule donc la probabilité d'une cause en fonction des
différentes probas conditionnelles de la "conséquence " B.

Note, je me rappelle avoir naîvement essayé de faire le calcul, que pour les processus stochastiques, ça ne marche pas.
Il n'y a pas de processus stochastique inverse mais juste du chaos..

en espérant ne pas avoir écrit trop de bêtises..

[Velandco]

D'accord merci je vais essayer d'appliquer ca, en espèrant réussir :triste:
Merci beaucoup en tous les cas!