J'ai déjà posé ce problème et personne ne peut y répondre... Je commence a me demander si la solution existe bel et bien (désolé pour ceux qui auront un gout de deja vu) :
le problème est le suivant, j'ai une fonction suivant une équation du type black and scholes, c'est à dire telle que
}{S(t)} = \mu * dt + \sigma dW_t)
où

est un mouvement brownien, et

et

sont des constantes connues.

On recherche
)_{t \alpha))
avec

une constante donnée.
piste : On montre « aisément » que si W(t) suit un mouvement Brownien standard, que
)
, Ceci grâce au raisonnement de symétrie, et la propriété de Markov faible.
Ce qui aide a trouver la solution lorsqu'il ny a pas de drift (ie :
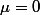
). mon gros probleme est donc le cas général ou

Si quelqu'un pouvait m'aider ca serait super gentil...
