Bonjour a vous
Jai besoin d'aide j'arrive pas a traite cet exercice
Exercice:
soit F la fonction de repartition d'une variable aleatoire reelle X .
1/ Montrer que l'ensemble D= {x € a R tel que F soit discontinue en x } est denombrable
2-Si F est continue montrer que la variable Y=F (X) est uniforment distrubuee sur [0,1] c'est a dire P (Y <= y)=y
pour tout y € a [0,1]
Besoin d'aide merci
Probabilités : fonction de repartition
5 messages
- Page 1 sur 1
Re: probabilités : fonction de repartition
Salut,
(1) La fonction de répartition d'une V.A.R., elle est croissante : pourquoi ?
(2) Donc elle admet des limites à droite et à gauche en tout points : preuve ?
(3) De plus, si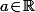 alors les 3 réels
alors les 3 réels \!=\!\lim_{x\to a^-}F(x)) ;
; \!=\!\lim_{x\to a^+}F(x)) et
et ) vérifient . . . donc en fait F est . . . et on a
vérifient . . . donc en fait F est . . . et on a \!-\!F(a^-)\!=\!) . . .
. . .
(4) L'ensemble des points de discontinuité de
des points de discontinuité de  c'est ceux tels que
c'est ceux tels que \!\not=\!F(a^-)) c'est à dire . . .
c'est à dire . . .
(5) En fait on a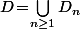 où
où 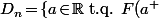\!-\!F(a^-)\!\geq\!\frac{1}{n}\}) : preuve ?.
: preuve ?.
(6) Or, pour tout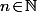 ,
, 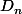 est fini (et même ...) car . . .
est fini (et même ...) car . . .
(7) Donc est au plus dénombrable car c'est . . .
est au plus dénombrable car c'est . . .
(1) La fonction de répartition d'une V.A.R., elle est croissante : pourquoi ?
(2) Donc elle admet des limites à droite et à gauche en tout points : preuve ?
(3) De plus, si
(4) L'ensemble
(5) En fait on a
(6) Or, pour tout
(7) Donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilités : fonction de repartition
1- elle est croissante en prenant a <b F (b)=F (a)+P (a <X <=b)>=F (a)
Re: probabilités : fonction de repartition
2- je pense que c'est parce qu'elle est croissante et bornee
Re: probabilités : fonction de repartition
3- cela verifie limite a gauche est egale a limite a droite ou bien ?
Donc si c'est le cas F est continue
4-je comprend pas
5-je comprend pas
6-fini et denombrable car en bijection avec Q ?
7-car c'est une reunion d'ensemble denombrable
Donc si c'est le cas F est continue
4-je comprend pas
5-je comprend pas
6-fini et denombrable car en bijection avec Q ?
7-car c'est une reunion d'ensemble denombrable
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
