Bonjour, j'ai un DM a faire (j'ai le temps rien d'urgent) et ça fait 1h que je tourne en rond sur le premier exercice. Voici l'énoncé:
On lance un dé 20 fois. Soit V la v.a. égale au nombre de cinq obtenus.
Déterminer la loi de V. Quelle est la probabilité dobtenir moins de 3 fois un cinq ?
C'est un exercice "bateau" mais je ne suis pas sûre de moi déjà pour le cardinal (noté U parce que je ne sais pas faire oméga sur le clavier) je pensais à 6^20 mais ça me parait beaucoup.
Pour la loi de V j'ai commencé par
V(U) = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
P[N=0] = (5^20)/card U
P[N=1] = (20/6) / card U
j'explique mon raisonnement, 1/6 pour le probabilité d'avoir un 5, fois 20 car on a 20 lancés et divisé par card U car c'estla méthode utilisé dans les autres exercice. Mon problème c'est que le résultat est supérieur à 1 donc je ne pense pas que mon raisonnement soit bon.
Est ce que quelqu'un veut bien m'expliquer d'où vient mon erreur s'il vous plaît?
Probabilité
11 messages
- Page 1 sur 1
Le Omega est ce que c'est l'ensemble des evenements possibles ou quelque chose d'autre deja (j'ai un petit trou de memoire) ?
Sinon ta variable n'est rien d'autre qu'une variable aleatoire suivant une loi Binomiale avec une probabilite de succes de 1/6 et un nombre de realisations de 20.
La suite doit ensuite venir toute seule.
Sinon ta variable n'est rien d'autre qu'une variable aleatoire suivant une loi Binomiale avec une probabilite de succes de 1/6 et un nombre de realisations de 20.
La suite doit ensuite venir toute seule.
Omega est bien l'ensemble des évènements possibles.
Mais pour moi la question posée n'était pas quelle est la probabilité d'avoir un 5 à tel ou tel lancé mais plutôt quelle est la probabilité d'avoir un seul (ou deux ou trois) 5 sur l'ensemble des lancés.
Je pensais utiliser le loi de X (ou loi hypergéométrique) mais je ne sais pas si elle est vraiment adaptée.
Mais pour moi la question posée n'était pas quelle est la probabilité d'avoir un 5 à tel ou tel lancé mais plutôt quelle est la probabilité d'avoir un seul (ou deux ou trois) 5 sur l'ensemble des lancés.
Je pensais utiliser le loi de X (ou loi hypergéométrique) mais je ne sais pas si elle est vraiment adaptée.
pour exemple tu recherches la proba d'obtenir 2 cinq sur les 20 lancés :
il y a pour cela C20,2 combinaisons qui permettent d'obtenir deux 5
calculons la proba d'obtenir un cinq au premier et au second lancé ,
d'apres la loi binomiale on écrirait P=C20,1.p.(1-p)^19.C20,2.P².(1-P)^18
avec p=1/6
mais comme il existe 190 combinaisons dans ce cas pour obtenir 2 cinq
alors on écrira P(V=2)=C20,1.p.(1-p)^19. SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 2 et 20 +C20,2..p².(1-p)^18.SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 3 et n +.......+C20,20.p^20.SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 20 et 20..... tu peux mettre tout ca en forme .
il y a pour cela C20,2 combinaisons qui permettent d'obtenir deux 5
calculons la proba d'obtenir un cinq au premier et au second lancé ,
d'apres la loi binomiale on écrirait P=C20,1.p.(1-p)^19.C20,2.P².(1-P)^18
avec p=1/6
mais comme il existe 190 combinaisons dans ce cas pour obtenir 2 cinq
alors on écrira P(V=2)=C20,1.p.(1-p)^19. SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 2 et 20 +C20,2..p².(1-p)^18.SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 3 et n +.......+C20,20.p^20.SOM(C20,k.P^k.(1-P)^(20-k)) pour k compris entre 20 et 20..... tu peux mettre tout ca en forme .
salut,
sois k le nombre de 5 qu'on a eu :
sur 20 lancers, tu as emplacements possibles pour placer tes 5 et donc
emplacements possibles pour placer tes 5 et donc  pour placer les autres chiffres.
pour placer les autres chiffres.
Tu passes un coup de proba dessus : 1/6 pour une reussite, 5/6 pour autre chose qu'un 5
Ca te donne donc
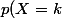=C_{20}^k (\frac{1}{6})^k C_{20}^{20-k} (\frac{5}{6})^{20-k})
Enfin, je ferais comme ca personnellement
sois k le nombre de 5 qu'on a eu :
sur 20 lancers, tu as
Tu passes un coup de proba dessus : 1/6 pour une reussite, 5/6 pour autre chose qu'un 5
Ca te donne donc
Enfin, je ferais comme ca personnellement
la vie est une fête 
Non il s'agit bien d'une loi geometrique et donc ton deuxieme element de commbinatoire (20-k parmi 20) est en trop fatal error.
Il serait interessant si l'on cherche a enumerer le nombre de cas favorable par rapport au nombre de cas total.
Mais ici en rajoutant de probabilites ce n'est pas de la meme facon que l'on doit raisonner
Il serait interessant si l'on cherche a enumerer le nombre de cas favorable par rapport au nombre de cas total.
Mais ici en rajoutant de probabilites ce n'est pas de la meme facon que l'on doit raisonner
salut,
tu as raison pour l'élément de combinaison.
Toutefois, j'opterais plutot pour une loi binomiale
 = P(X = k)= C_n^k \times p^k q^{n-k})
avec p=1/6 et q=5/6
tu as raison pour l'élément de combinaison.
Toutefois, j'opterais plutot pour une loi binomiale
On renouvelle n fois de manière indépendante une épreuve de Bernoulli de paramètre p...
On compte alors le nombre de succès obtenus à l'issue des n épreuves et on appelle X la variable aléatoire correspondant à ce nombre de succès.
avec p=1/6 et q=5/6
la vie est une fête 
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
