Probabilite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
balba
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Oct 2008, 21:20
-
 par balba » 23 Oct 2008, 21:28
par balba » 23 Oct 2008, 21:28
Bonjour,
Petite question de proba:
Si X est une variable aleatoire a valeur discrete dont on connait la distribution (donc on connait P(X=n) pour tout n), et que An est l'evenement "n divisie X", que peut-on dire de P(An) si n est premier?
Est-ce vrai que P(An)=P(X=n*1 ou X=n*2 ou X=n*3 ...)=Somme sur k des P(X=nk)?
Merci.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 23 Oct 2008, 22:13
par yos » 23 Oct 2008, 22:13
Oui. C'est encore vrai si n est pas premier.
-
balba
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Oct 2008, 21:20
-
 par balba » 23 Oct 2008, 23:51
par balba » 23 Oct 2008, 23:51
Merci.
Et a-t-on bien P(intersection de tous les An, n premier)=P(tous les nombres premiers divisent X)=P(X=0)?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Oct 2008, 11:47
par yos » 24 Oct 2008, 11:47
Oui c'est juste.
-
balba
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Oct 2008, 21:20
-
 par balba » 24 Oct 2008, 21:11
par balba » 24 Oct 2008, 21:11
Hum...en fait c'est plutot P(X different 1, X different de 2,...)=Produit sur k des 1-P(X=k).
En fait, je cherche a prouver le produit d'Euler: 1/Zeta(s)=Produit sur p premier des (1-1/p^s), et utilisant l'independence des Ap, p premier, et la distribution P(X=n)=n^(-s)/Zeta(s).
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Oct 2008, 09:08
par yos » 25 Oct 2008, 09:08
balba a écrit:Et a-t-on bien P(intersection de tous les An, n premier)=P(tous les nombres premiers divisent X)=P(X=0)?
Enlève ton P :

est l'événement (X=0).
Mais je doute que ça te donne l'égalité d'Euler, laquelle résulte d'un simple calcul.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Oct 2008, 20:24
par yos » 25 Oct 2008, 20:24
En effet! Je connaissais pas.
Calcule
)
de deux façons différentes sachant que les

sont mutuellement indépendants.
-
balba
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Oct 2008, 21:20
-
 par balba » 26 Oct 2008, 12:08
par balba » 26 Oct 2008, 12:08
Ah merci, c'est tout simple.
Pour la derniere question je suis tente d'ecrire:
P(n est PGCD de X,Y)=P({n divise X} et {n divise Y} et {pour tout p premier, p ne divise pas a la fois X/n et Y/n}) mais le dernier evenement n'est pas forcement independent...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Oct 2008, 16:48
par yos » 26 Oct 2008, 16:48
On a
=P((n|X)\cap (n|Y))=P(A_n)^2=n^{-2s})
et je vois pas pour P(D=n). Par rapport à P(D|n) il n'y a que
)
en plus au dénominateur. Ca donne envie d'utiliser la question 2 mais je ne vois pas de lien. J'y réfléchis.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Oct 2008, 17:21
par yos » 26 Oct 2008, 17:21
Je le tiens en écrivant :
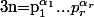
,
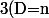=\left(\bigcap_{i=1}^r(p_i^{\alpha_i}|X) \cap (p_i^{\alpha_i+1}\not{|}X)\cap (p_i^{\alpha_i}|Y)\cap (p_i^{\alpha_i+1}\not{|}Y)\right) \cap \left(\bigcap_{p\in \mathcal{P},p\neq p_i}P(\bar{A_p})\right))
.
C'est lourd mais plus simple que ça en a l'air. La probabilité de
 \cap (p_i^{\alpha_i+1}\not{|}X))
s'obtient par simple soustraction.
-
balba
- Membre Naturel
- Messages: 10
- Enregistré le: 23 Oct 2008, 21:20
-
 par balba » 26 Oct 2008, 19:31
par balba » 26 Oct 2008, 19:31
Tiens oui decomposer n...
Que veux tu dire par simple soustraction? Je vois peu de simplifications.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Oct 2008, 21:08
par yos » 26 Oct 2008, 21:08
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
