Probabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 10 Mai 2015, 17:10
par humbug » 10 Mai 2015, 17:10
Salut !
Bon je suis en pleine révision pour mes partiel et la je suis pris d'un gros doute

je suis en train de faire l'exercice 2
je ne suis pas sur d'une chose,
quand on parle de P(D/ /A), on parle bien de la probabilité de chopper un CD defectueux dans le la pourcentage de boite non abimé,
du coup la probabilité se calcule sur les 100% des boites, ou sur les 95% restante (donc les 98% ou
93.1%)
par contre pour la question 2 je m'embrouille complètement la tête
je n'arrive pas a trouver le bon raisonnement pour le convertir mathématiquement...
voila merci d'avance

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 10 Mai 2015, 18:19
par chombier » 10 Mai 2015, 18:19
humbug a écrit:Salut !
Bon je suis en pleine révision pour mes partiel et la je suis pris d'un gros doute

je suis en train de faire l'exercice 2
je ne suis pas sur d'une chose,
quand on parle de P(D/ /A), on parle bien de la probabilité de chopper un CD defectueux dans le la pourcentage de boite non abimé,
du coup la probabilité se calcule sur les 100% des boites, ou sur les 95% restante (donc les 98% ou
93.1%)
par contre pour la question 2 je m'embrouille complètement la tête
je n'arrive pas a trouver le bon raisonnement pour le convertir mathématiquement...
voila merci d'avance
)
, aussi écrit
)
, c'est la probabilité que l'événement D se réalise SACHANT que l'événement A se réalise.
Il y a une formule pour ça :
 = P_B(A) = \frac {P(A \cap B)}{P(B)})
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 10 Mai 2015, 19:49
par humbug » 10 Mai 2015, 19:49
chombier a écrit:)
, aussi écrit
)
, c'est la probabilité que l'événement D se réalise SACHANT que l'événement A se réalise.
Il y a une formule pour ça :
 = P_B(A) = \frac {P(A \cap B)}{P(B)})
merci de me repondre
Je connais déjà c'est formule. mais si j'ai bien compris ton message, p(D) sachant A se calcul donc bien sur le nombre de boite abimé, et pas le nombre de boite totale
pour la question 2 si j'ai bien compris, il faut que je calcule P(A/D)=p(DnA)/P(D)
si j'ai bien tout comprit, je peut dire que P(DnA)=P(AnD), dans ce cas j'obtient 3%
(peut on appliquer la formule P(AnB)= P(a) * p(B) dans ce cas la ?)
mais comment calculer p(D) ?

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 10 Mai 2015, 20:15
par chombier » 10 Mai 2015, 20:15
humbug a écrit:merci de me repondre
Je connais déjà c'est formule. mais si j'ai bien compris ton message, p(D) sachant A se calcul donc bien sur le nombre de boite abimé, et pas le nombre de boite totale
pour la question 2 si j'ai bien compris, il faut que je calcule P(A/D)=p(DnA)/P(D)
si j'ai bien tout comprit, je peut dire que P(DnA)=P(AnD), dans ce cas j'obtient 3%
(peut on appliquer la formule P(AnB)= P(a) * p(B) dans ce cas la ?)
mais comment calculer p(D) ?
Je ne comprends pas bien les notations de ton exercice en fait :
)
c'est la probabilité de D sachant A, mais
)
, est-ce la probabilité de

(l'antislash serait à l'envers ?), autrement dit de

.
On aurait :
 = P(D - \bar{A}) = P(D \cap A))
?
Sinon, pour ta question, p(D) c'est la probabilité qu'une disquette (un CD-ROM ?) soit défectueuse, donc 0,6 d'après l'énoncé.
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 10 Mai 2015, 20:25
par humbug » 10 Mai 2015, 20:25
chombier a écrit:Je ne comprends pas bien les notations de ton exercice en fait :
)
c'est la probabilité de D sachant A, mais
)
, est-ce la probabilité de

(l'antislash serait à l'envers ?), autrement dit de

.
On aurait :
 = P(D - \bar{A}) = P(D \cap A))
?
Sinon, pour ta question, p(D) c'est la probabilité qu'une disquette (un CD-ROM ?) soit défectueuse, donc 0,6 d'après l'énoncé.
l'enoncer que tu voie est l'examen de l'année derniere,
je pense que la notation
)
et
)
veulent dire la meme chose, et ce serait juste un piege.
par contre, P(D) c'est bien le pourcentage de CD defectueux, mais uniquement dans les boite abimé, il y a aussi 0.02 de CD defectueux dans les boite non abimé :hein:
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 10 Mai 2015, 20:29
par marawita1 » 10 Mai 2015, 20:29
chombier a écrit:Je ne comprends pas bien les notations de ton exercice en fait :
)
c'est la probabilité de D sachant A, mais
)
, est-ce la probabilité de

(l'antislash serait à l'envers ?), autrement dit de

.
On aurait :
 = P(D - \bar{A}) = P(D \cap A))
?
Sinon, pour ta question, p(D) c'est la probabilité qu'une disquette (un CD-ROM ?) soit défectueuse, donc 0,6 d'après l'énoncé.
Je pense pas que la probabilité p(D) est 0,6, à mon avis p(D)= (0,05 x 0,6) + (0,95 x 0,02)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 10 Mai 2015, 20:49
par chombier » 10 Mai 2015, 20:49
marawita1 a écrit:Je pense pas que la probabilité p(D) est 0,6, à mon avis p(D)= (0,05 x 0,6) + (0,95 x 0,02)
Exact,
 = p(D \cap A) + p(D \cap \bar{A}) = p(A) p_A(D) + p(\bar{A}) p_{\bar{A}}(D))
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 10 Mai 2015, 21:24
par humbug » 10 Mai 2015, 21:24
chombier a écrit:Exact,
 = p(D \cap A) + p(D \cap \bar{A}) = p(A) p_A(D) + p(\bar{A}) p_{\bar{A}}(D))
Nickel, tout est clair pour cet exo, j'aurais d'autre question concernant l'exo 1, pour celui ci j'ai la solution de l'exo, mais il y as un passage que je ne comprend pas du tout.
je vais tout poster a la suite mais au besoin j'ouvrirais un autre sujet :

je ne comprend pas la simplification de la loi binomiale ...

et également ou est passer l'exposant n du dénominateur a la dernière ligne
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 10 Mai 2015, 21:52
par marawita1 » 10 Mai 2015, 21:52
humbug a écrit:Nickel, tout est clair pour cet exo, j'aurais d'autre question concernant l'exo 1, pour celui ci j'ai la solution de l'exo, mais il y as un passage que je ne comprend pas du tout.
je vais tout poster a la suite mais au besoin j'ouvrirais un autre sujet :

je ne comprend pas la simplification de la loi binomiale ...

et également ou est passer l'exposant n du dénominateur a la dernière ligne
A quoi est égale la quantité (a + b)^n , pour a et b réels?
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 11 Mai 2015, 15:39
par humbug » 11 Mai 2015, 15:39
marawita1 a écrit:A quoi est égale la quantité (a + b)^n , pour a et b réels?
Autant pour moi je ne connaissais pas la formule pour une identité remarquable de rang n
et la derniere ligne alors ? l'exposant il est partie ou ?
-
marawita1
- Membre Relatif
- Messages: 185
- Enregistré le: 16 Fév 2015, 19:12
-
 par marawita1 » 11 Mai 2015, 16:30
par marawita1 » 11 Mai 2015, 16:30
humbug a écrit:Autant pour moi je ne connaissais pas la formule pour une identité remarquable de rang n
Formule de binôme
et la derniere ligne alors ? l'exposant il est partie ou ?
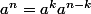
-
humbug
- Messages: 6
- Enregistré le: 10 Mai 2015, 16:44
-
 par humbug » 16 Mai 2015, 11:15
par humbug » 16 Mai 2015, 11:15
Tout est bon du coup merci a vous ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités



