pluie2 a écrit:donc P(X=3):
PPPFFFFF
PPFFFFFP
PFFFFFPP
FFFFFPP
...
A part le premier, tout tes autres "cas" sont faux vu qu'on obtient 5 Faces avant la fin.
Par exemple, il est impossible d'avoir PPFFFFFP vu qu'arrivé à PPFFFFF on a déjà 5 Faces donc la partie s'arrête (et en plus elle s'arrête avec X=2 et pas avec X=3 vu qu'on a que 2 Piles)
pluie2 a écrit:n'y aurait il pas une méthode plus rigoureuse pour trouver directement le résultat car ça prend beucoup de temps et le but dans ce genre d'exo c'est jstement d'aller vite nan?
Bien sûr.
Si

pour avoir
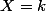
, c'est forcément que la partie c'est terminé avec 5 Faces (vu que k<4) donc on a jeté la pièce 5+k fois, on a obtenu k Piles et 5 Faces et
on a forcément fini par un Face (sinon la partie se serait terminée avant)
Donc chacun des tirages conduisant à
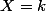
a une proba de
^{5+k})
(on jette forcément 5+k dés) et il faut calculer le nombres de tirages, c'est à dire le nombre de façons de répartir les k Piles parmi les 5+k tirages sachant que le dernier ne doit pas être Pile. Donc il faut en fait répartir les k Piles parmi les 4+k tirages autres que le dernier et il y a

(coefficient binomial) possibilités.
Conclusion
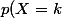=\binom{4+k}{k}(\frac{1}{2})^{5+k})
Pour
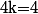
, il y a deux solutions :
- Soit on est sûr de son coup concernant le calcul ci dessus est on dit que
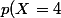=1-p(X=0)-p(X=1)-p(X=2)-p(X=3))
.
- Soit on a des doute et on essaye de trouver une autre méthode permettant de vérifier à la fin que la somme des proba fait bien 1 :
Pour avoir X=4, il faut avoir tiré 4 Piles,
que le dernier tirage soit un Pile (sinon le jeu se serait arrête avant) et un nombre

de Faces.
En raisonnant comme ci dessus, on voit que, pour tout

,
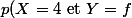=\binom{3+f}{f}(\frac{1}{2})^{4+f}\ \)
et donc
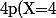=\sum_{f=0}^4\binom{3+f}{f}(\frac{1}{2})^{4+f})
