Probabilité : nombre de tirages variable

[sjfeg]

Bonjour,

J'ai une urne avec 70 boules noires, 5 boules blanches et 1 boule rouge. J'ai un compteur de tirage initialisé avec la valeur 3. Les tirages sont sans remise. Si je tire une boule noire, mon compteur est décrémenté d'une unité. Si je tire une boule blanche il est incrémenté de 2 unités. Si je tire la boule rouge j'ai gagné. Quand mon compteur est à 0, j'arrête de tirer. Je cherche à calculer la probabilité de gagner. :mur:

Tout conseil sur la manière d'aborder le problème sera le bienvenu.

D'avance merci,

Jef

[Ben314]

Salut,
Je ne vois qu'une façon "empirique" de le faire (par exemple avec un tableur).
Pour tout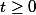 (entier) notons
a) la proba. d'avoir perdu au t-ième tirage (ou avant).
b) Pour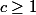 , la proba de n'avoir ni gagné, ni perdu au t-ième tirage et d'avoir c "points" au compteur.
c) la proba d'avoir gagné au t-ième tirage (ou avant).
Évidement, la somme pour un t donné doit faire 1 et on part, pour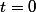 avec et tout le reste nul.

Aprés, tu arrive relativement facilement à calculer les et en fonction des et de car :
Si tu sait qu'au t-ième tirage ton compteur vaut c, cela signifie que, si on note b et n le nombre de boules blanches et noires déjà tirées, on a t=b+n et c=3+2b-n donc tu peut en déduire b et n puis le nombre de boules noires et blanches restant dans l'urne et donc les proba de passer de "l'état" (t,c) à "l'état" (t+1,?).

[DamX]

Hello,

je pense que la solution de Ben marche très bien. Je propose juste une autre manière de poser le problème :

Si P(n,b) est la probabilité de gagner lorsqu'on a la boule rouge, n boule noire et b blanches dans le pot, on a la relation (à justifier) :

P(n,b) = (1 + n*P(n-1,b) + b*P(n,b-1)) / (1+n+b)
Avec la condition au bord que P(n,b) = 0 dès lors que 3-(70-n)+2(5-b) <= 0, ie quand n-2b <= 57.


Partant de là un tableur va très bien faire ça en effet.

Le truc intéressant c'est qu'on peut voir que si on pose U(b,n) = (1+n+b)!/58! * P(b,n), U se résout de manière similaire mais est toujours à valeurs entières (et la division par 58! est là pour contenir tant bien que mal l'explosion des termes), ce qui, sauf erreur de ma part ou mauvaise manipulation d'excel avec des nombres entiers qui avoisinent tout de même les 10^20 au cours des calculs permet d'obtenir une expression exacte de la proba :
P(70,5) = 195804753855977 / 4010732833414290 ~ 4.88%

Bon mais sinon si les tableurs sont interdits, avec un peu de patience et de rigueur ( :mur: ) ça se fait à la calculette vu qu'il y a "seulement" une petite 50 aine de termes à calculer :ptdr:

Damien

[sjfeg]

Bonsoir,

Un grand merci à vous 2 :zen:

Ben, j'ai implémenté la méthode récursive que tu suggères et j'ai effectivement trouvé 4,88%

Damien, je suis impressionné par la simplicité de ta formule de récurrence qui va en plus me permettre de répondre à une autre question que je me pose : n étant fixé, combien de boules blanches pour que la probabilité de gagner soit d'environ 25%. Cela étant, je ne suis pas encore convaincu de sa démonstration :hein:

[sjfeg]

Damien,

Et la lumière fut ... C'est la condition de bord de P(n,b) qui assure que le compteur de tirage est positif. Très élégant !

[Ben314]

Le truc intéressant c'est qu'on peut voir que si on pose U(b,n) = (1+n+b)!/58! * P(b,n)...

Si tu veut que ça explose un peu moins vite, tu peut poser
V(n,b) = p(n,b) * (n+b+1)! / (n! * b!)

Ca donne V(n,b)=binom(n+b,b)+V(n,b-1)+V(n-1,b) (donc ça reste entier)
où binom(n+b,b) est le coefficient binomial.

Dans le cas 70, 5 ça donne la fraction 64 038 114 / 1 311 713 640 un peu plus petite que la tienne.

[DamX]

Si tu veut que ça explose un peu moins vite, tu peut poser
V(n,b) = p(n,b) * (n+b+1)! / (n! * b!)

Ca donne V(n,b)=binom(n+b,b)+V(n,b-1)+V(n-1,b) (donc ça reste entier)
où binom(n+b,b) est le coefficient binomial.

Dans le cas 70, 5 ça donne la fraction 64 038 114 / 1 311 713 640 un peu plus petite que la tienne.

Hello,

Ca a l'air bon ton truc, par contre du coup je dois avoir une erreur de calcul dans ma fraction peut etre liée aux limites du tableur quia fait des arrondis à un certain nombre de chiffres significatifs, parce qu'elle était irréductible ma fraction selon wolfram...

Damien

[Ben314]

Hello,
Ca a l'air bon ton truc, par contre du coup je dois avoir une erreur de calcul dans ma fraction peut etre liée aux limites du tableur quia fait des arrondis à un certain nombre de chiffres significatifs, parce qu'elle était irréductible ma fraction selon wolfram...
Damien

Sur le "principe" (i.e. la formule de récurrence) je suis à peu prés sûr de mon coup, mais après, il est tout à fait possible que je me soit gouré avec le tableur... (j'ai juste vérifié que ça donnait à peu prés les 4.88 % dont tu parlais...)

Edit : Quoi que...
1 311 713 640 / 64 038 114 * 195 804 753 855 977 vaut (à l'unité prés) 4 010 732 833 414 294 qui est quand même vraiment très proche de ton 4 010 732 833 414 290 (4 unités de moins...)
Et comme ton dénominateur se termine par '0', ça ressemble fort à un arrondi...