Probabilité et intégration

[Als128]

Bonjour à tous,

Je bloque sur un problème de proba. J'ai la solution (car mon bouquin d'exo est corrigé) mais je comprends pas le raisonnement. L'énoncé est :
Soit , P la loi uniforme sur et soit sur X la variable aléatoire X(x,y)=x+y
1)Calculer E(X)
2)Determiner la loi de X sur [0,2] et en déduire E(X).

Si une ame charitable familière avec les concepts utilisés pouvaient m'aider... Merci !

[Nightmare]

Que ne comprends-tu pas dans la correction? A priori c'est une simple application des formules du cours !

[Als128]

:we: j'ai jamais dit que c'était compliqué, j'ai dit que je comprenais pas la solution :id:
La solution écrit (pour la question 2, parce que la 1 c'est bon)

Soit une fonction mesurable bornée, on a :

avec le changement de variable



Donc la loi de est de densité avec sur et sur et :

première chose que je ne comprends pas : a quoi correspond ?
deuxième chose : pourquoi ça donne
troisième chose : comment le changement de variable donne

Enfin, dans la question je comprend pas à quoi correspond l'intervalle

Petite précision en ce qui me concerne : je suis des cours de 1ere école d'ingé par correspondance dans le cadre de ma formation professionnelle. Ma prépa remonte à 2002... donc je suis un peu rouillé :hein: Comme pour le moment j'ai aucun prof pour répondre à mes questions (mais c'est qu'une question de tps) je rame un peu avec certains concepts que je (re)découvre.

Merci de ton aide !

[Als128]

Ou alors m'expliquer ton raisonnement pour la solution... J'aimerais juste comprendre...

[Boss38100]

c'est la fonction caractéristique si je me rappel bien essaye de voir là

[Als128]

Merci pour ton lien, mais je crois qu'il m'a encore plus interrogé :doh: En fait le truc c'est que je ne comprends absolument pas toutes les phases du raisonnement. Quand au wiki sur la fonction caractéristique, j'arrive pas à faire le lien avec l'exo (surtout qu'elle n'a pas encore été évoquée dans mon cours)

Bref, mes questions restent posées... J'aimerais bien comprendre cette p*%§@$ de solution. Ou à défaut, si quelqu'un à un autre mode de raisonnement qu'il me l'explique pas à pas.

Parce que buter sur un exercice comme ça ça me décourage un peu...

Voilà !

[Joker62]

Bonjour,

Une première étape pour ton problème, c'est le théorème suivant :

Une variable aléatoire X admet p pour densité de proba Pour toute fonction h mesurable positive, on a

La fonction Phi elle est donc là pour ça (La correction l'a choisie mesurable bornée parce que les fonctions bornées sont intégrales sur les espaces de mesures finies ( et comme on est sur un espace de probas, c'est forcément de mesure finie) et que dans le cas ou la fonction est mesurable positive, elle est toujours intégrable mais dans le sens ou elle peut valoir +;), enfin c'est d'la théorie de l'intégration, on s'en fiche un peu)

Donc à partir de ce théorème le reste en découle. Sauf que c'est mal écrit dans la correction.

[Als128]

Merci !!! C'est bon j'ai compris l'apparition de la fonction et son utilité ! Merci beaucoup !!!

Par contre, pourquoi l'intégrale de y à 1+y ? C'est quoi la signification ?

[Joker62]

Je vois pas trop.

Les hypothèses sont bien : x et y des variables aléatoires indépendante de loi uniforme sur [0;1]

Et on pose X = x+y ?

[Als128]

Soit , P la loi uniforme sur et soit sur X la variable aléatoire X(x,y)=x+y
1)Calculer E(X)
2)Determiner la loi de X sur [0,2] et en déduire E(X).

Si une ame charitable familière avec les concepts utilisés pouvaient m'aider... Merci !

J'ai bien regardé, l'exercice en dit pas plus. en particulier, il ne precise pas si x et y sont des variables aléatoires indépendante...

[Joker62]

Soit c'est un livre de sado-masochiste, soit c'est un physicien qui l'a écrit (Pardon Domi , c'était pour la blague :p)

En fait le problème revient dans le fait que




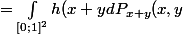Et là si on a pas l'hypothèse d'indépendance, on peut pas continuer.
Donc on va les supposer indépendantes

parce que x et y suivent des lois uniformes sur [0;1]

Maintenant on va faire un changement de variable (Il faut que ce soit un C^1-difféo donc on aura une application J : R^2 -> R^2) Mais comme on doit passer de (x,y) à x+y, on va devoir poser par exemple :

J : [0;1]^2 -> Delta ; qui a (x,y) associe (x;x+y) (On envoie x sur x)

On a J^-1 : Delta -> [0;1]^2 qui a (u,v) associe (u;v-u)

Pour arriver dans les bon ensembles, on doit avoir Delta = {(u,v) | u € [0;1] et v-u€[0;1]}

Mais v-u € [0;1] v € [u;u+1]

Et tu peux effetuer ton changement de variable tranquillement, en utilisant Fubini pour la suite.

[yos]

Soit , P la loi uniforme sur et soit sur X la variable aléatoire X(x,y)=x+y
1)Calculer E(X)
2)Determiner la loi de X sur [0,2] et en déduire E(X).

La loi de X, c'est la connaissance des pour chaque réel a de [0,2].
Tu dessines le carré [0,1]X[0,1] . Dans ce carré, un point M(x,y) a une probabilité d'être dans une région donnée proportionnelle à l'aire de cette région (loi uniforme).
Dire que M appartient à l'événement , c'est dire que , ou encore que M est en dessous de la droite d'équation y=a-x. Le tracé de cette droite montre bien qu'il y a deux cas.
- Si , l'événement est un triangle rectangle isocèle d'aire a²/2. On a donc .

-, l'événement est le carré tronqué d'un triangle isocèle d'aire . .

Après on peut faire plus savant (et raconter n'importe quoi aussi).

[Als128]

Soit c'est un livre de sado-masochiste, soit c'est un physicien qui l'a écrit (Pardon Domi , c'était pour la blague :p)

Ben en fait...non mais l'impression date de 89 à l'époque l'ordinateur était rare et moins on mettait de lignes moins c'était couteux. Les explications sont très concises. Donc pour ton laius de 15 lignes, le bouquin n'explique rien... C'est peut être évident pour des gens qui baignent dedans tous les jours mais moi je rame énormément. Donc un grand merci pour ton aide !!!

C'est bon j'ai compris le coup du changement de variable et du calcul qui s'en rapporte !
Merci :++:

[yos]

l'exercice ne precise pas si x et y sont des variables aléatoires indépendante...

Dire que la loi sur est uniforme entraîne cela.

[yos]

...et raconter n'importe quoi aussi.

cela dit sans viser personne bien sûr, sauf peut-être l'auteur du livre d'où est tiré le corrigé que nous a fourni Als 128.