Bonjour à tous,
Mon problème n'est pas un problème scolaire mais un problème personnel, et je ne savais pas dans quel catégorie le mettre. Vous pouvez le déplacer si besoin.
J'aimerai savoir comment calculer une probabilité P(X | Y=y) (probabilité de X sachant que Y est égal à y) lorsque X est une variable aléatoire discrète et que Y est une variable aléatoire continue.
Je suis intéressé par le cas général, mais je vais vous donner un cas d'application pour simplifier la compréhension :
On a 2 moutons.
Lorsque le premier bêle, l'intensité du bêlement en décibels est représentée par une variable aléatoire M1 qui suit une loi normale N(m1, s1 ^ 2)
Lorsque le second bêle, l'intensité du bêlement en décibels est représentée par une variable aléatoire M2 qui suit une loi normale N(m2, s2 ^ 2)
L'un des 2 moutons bêle, mais on ne sait pas lequel.
On note X l’événement: Le premier mouton a bêlé
On sait qu'il y a une probabilité à priori p pour que ce soit le premier mouton qui ait bêlé, donc P(X)=p et P(non X)=1-p
On mesure l'intensité du bêlement, et on obtient une valeur d.
Tous les paramètres m1, s1, m2, s2, p et d sont connus.
On cherche à calculer la probabilité à posteriori que ce soit le premier mouton qui ait bêlé, sachant l'intensité mesurée.
D'après moi, on peut noter D = M1*p + M2*(1-p) la variable aléatoire du bêlement dont on ne connaît pas l'origine.
On cherche donc à calculer la probabilité P(X | D=d).
Si on applique naïvement la formule de Bayes, on a :
P(X | D=d) = P(D=d | X) * P(X) / P(D=d)
Le problème est que D étant une variable continue, on a P(D=d | X) = P(D=d) = 0.
On aurait donc P(X | D=d) = 0 / 0 qui n'est pas défini.
Comment puis-je faire pour calculer la probabilité voulue ?
Je précise que je ne suis actuellement plus en études, et malgré avoir été plutôt bon en mathématiques, je n'ai pas suivie de cursus poussé dans ce domaine.
J'espère avoir le niveau pour comprendre les réponses, mais soyez indulgents s'il vous plait x)
Je remercie par avance ceux qui prendront le temps de me répondre.
Probabilité discrète et continue
6 messages
- Page 1 sur 1
Re: Probabilité discrète et continue
Salut,
Il me semble que le problème, c'est qu'en général) (probabilité d'avoir
(probabilité d'avoir  sachant
sachant  , c'est défini comme étant égal à
, c'est défini comme étant égal à }{p(B)}) et, bien évidement, il faut que
et, bien évidement, il faut que \not=0) pour que ça ait du sens.
pour que ça ait du sens.
Or, si est une loi continue on va avoir
est une loi continue on va avoir =0) pour tout
pour tout  ce qui pose problème.
ce qui pose problème.
Donc si on veut espérer définir quelque chose de cohérent, je pense qu'il faut étendre la définition de proba conditionnelle en posant par exemple=\lim_{\varepsilon\to 0^+}p(X\,|\,|Y\!-\!y|\!<\!\varepsilon)) , mais à mon avis, il faut faire gaffe vu que c'est pas certain à 100% que ça fonctionne bien comme on pourrait l'espérer cette nouvelle définition (par exemple, ne pas utiliser des théorèmes "classiques" concernant les probas conditionnelles sans avoir pris soins de vérifier qu'ils restent corrects avec cette nouvelle définition)
, mais à mon avis, il faut faire gaffe vu que c'est pas certain à 100% que ça fonctionne bien comme on pourrait l'espérer cette nouvelle définition (par exemple, ne pas utiliser des théorèmes "classiques" concernant les probas conditionnelles sans avoir pris soins de vérifier qu'ils restent corrects avec cette nouvelle définition)
Donc dans le cas de tes moutons, plutôt que d'utiliser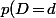) (qui est nul), tu prend à la place
(qui est nul), tu prend à la place ) qui est équivalent, lorsque
qui est équivalent, lorsque  , à
, à ) où
où  est la fonction de densité de
est la fonction de densité de  .
.
Idem pour=p(M_1\!=\!d)) que tu remplace par
que tu remplace par \sim2\varepsilon f_1(d)) où
où  est la fonction de densité de
est la fonction de densité de 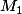 .
.
Et le bilan, c'est qu'en fait, tu décrète que}{p(D\!=\!d)}=\dfrac{f_1(d)}{f_D(d)}) ce qui va te dit que la proba que ce soit le 1er qui bêle est
ce qui va te dit que la proba que ce soit le 1er qui bêle est }{pf_1(d)\!+\!(1\!-\!p)f_2(d)}) et la proba que ce soit le 2nd est
et la proba que ce soit le 2nd est f_2(d)}{pf_1(d)\!+\!(1\!-\!p)f_2(d)})
Il me semble que le problème, c'est qu'en général
Or, si
Donc si on veut espérer définir quelque chose de cohérent, je pense qu'il faut étendre la définition de proba conditionnelle en posant par exemple
Donc dans le cas de tes moutons, plutôt que d'utiliser
Idem pour
Et le bilan, c'est qu'en fait, tu décrète que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probabilité discrète et continue
Merci pour ton explication.
J'avais effectivement pensé à passer par des limites, mais je ne savais pas comment le faire correctement sans faire n'importe quoi XD
Pour l'équivalence \sim 2\varepsilon f_D(d)) je la comprend intuitivement (on considère que la fonction
je la comprend intuitivement (on considère que la fonction  est constante aux alentours de d), mais je ne sais pas comment la démontrer, et surtout j'ai l'impression que ce n'est pas forcément vrai dans un cas général.
est constante aux alentours de d), mais je ne sais pas comment la démontrer, et surtout j'ai l'impression que ce n'est pas forcément vrai dans un cas général.
Est-ce que c'est une équivalence vraie uniquement dans le cas d'un loi normale comme dans mon exemple, ou bien c'est vrai pour n'importe quelle fonction de densité ?
Aussi, pour le dénominateur de la probabilité finale :\!+\!(1\!-\!p)f_2(d)) , je pense que ça vient du fait que j'ai dit dans mon premier message que
, je pense que ça vient du fait que j'ai dit dans mon premier message que ) , mais j'ai finalement l'impression que c'est faux. On aurai plutot :
, mais j'ai finalement l'impression que c'est faux. On aurai plutot :

Est-ce que j'ai bon là dessus ? Et si oui, comment adapter la probabilité finale ? Ça me semble plus compliqué à faire dans un cas conditionnel comme celui-ci.
J'ai aussi une autre question. Tu dis qu'on doit redéfinir la notion de probabilité conditionnelle en posant une nouvelle définition basée sur une limite. Mais est-ce que cette nouvelle définition correspond à la réalité d'un point de vue statistique ? C'est à dire que si je fais le calcul avec cette nouvelle définition, et que je réalise l'expérience des moutons un grand nombre de fois, est-ce que les résultats vont effectivement converger vers la solution théorique ?
Je pourrai faire une petite simulation en python pour le tester, et je vais probablement le faire, mais je voulais savoir si tu avais une raison de penser que c'est effectivement le cas, et si c'est démontrable ?
J'avais effectivement pensé à passer par des limites, mais je ne savais pas comment le faire correctement sans faire n'importe quoi XD
Pour l'équivalence
Est-ce que c'est une équivalence vraie uniquement dans le cas d'un loi normale comme dans mon exemple, ou bien c'est vrai pour n'importe quelle fonction de densité ?
Aussi, pour le dénominateur de la probabilité finale :
Est-ce que j'ai bon là dessus ? Et si oui, comment adapter la probabilité finale ? Ça me semble plus compliqué à faire dans un cas conditionnel comme celui-ci.
J'ai aussi une autre question. Tu dis qu'on doit redéfinir la notion de probabilité conditionnelle en posant une nouvelle définition basée sur une limite. Mais est-ce que cette nouvelle définition correspond à la réalité d'un point de vue statistique ? C'est à dire que si je fais le calcul avec cette nouvelle définition, et que je réalise l'expérience des moutons un grand nombre de fois, est-ce que les résultats vont effectivement converger vers la solution théorique ?
Je pourrai faire une petite simulation en python pour le tester, et je vais probablement le faire, mais je voulais savoir si tu avais une raison de penser que c'est effectivement le cas, et si c'est démontrable ?
Re: Probabilité discrète et continue
En fait je me rend compte que cela revient à poser dans un cas général pour une loi X de densité f, 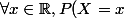 = f(x)) .
.
C'est bien évidemment faux écrit comme cela, mais en le posant ainsi et en utilisant la formule de Bayes, on retrouve bien la probabilité énoncée :
 = \frac{P(D=d | X) * P(X)}{P(D=d | X) * P(X) + P(D=d | \overline{X}) * P(\overline{X})} = \frac{P(M1=d) * P(X)}{P(M1=d) * P(X) + P(M2=d) * (1-P(X))} = \frac{pf1(d)}{pf1(d) + (1-p)f2(d)})
C'est bien évidemment faux écrit comme cela, mais en le posant ainsi et en utilisant la formule de Bayes, on retrouve bien la probabilité énoncée :
Re: Probabilité discrète et continue
Lorsque tu as une variable aléatoirequent217 a écrit:Pour l'équivalenceje la comprend intuitivement (on considère que la fonction
est constante aux alentours de d), mais je ne sais pas comment la démontrer, et surtout j'ai l'impression que ce n'est pas forcément vrai dans un cas général.
Est-ce que c'est une équivalence vraie uniquement dans le cas d'un loi normale comme dans mon exemple, ou bien c'est vrai pour n'importe quelle fonction de densité ?
Je pense que c'est la même chose.quent217 a écrit:On aurai plutot :
Est-ce que j'ai bon là dessus ? Et si oui, comment adapter la probabilité finale ? Ça me semble plus compliqué à faire dans un cas conditionnel comme celui-ci.
De tout façon, j'ai l'impression que tu ne peut rien calculer si tu connait uniquement les lois de
Et si tu as cette info. concernant la proba. que ce soit le premier qui bêle, alors ta loi
modulo de supposer tout les événements indépendants.
Je suis persuadé que ça fonctionne parfaitement, en particulier du fait que des proba telles quequent217 a écrit:J'ai aussi une autre question. Tu dis qu'on doit redéfinir la notion de probabilité conditionnelle en posant une nouvelle définition basée sur une limite. Mais est-ce que cette nouvelle définition correspond à la réalité d'un point de vue statistique ? C'est à dire que si je fais le calcul avec cette nouvelle définition, et que je réalise l'expérience des moutons un grand nombre de fois, est-ce que les résultats vont effectivement converger vers la solution théorique ?
Et concernant le fait que "c'est démontrable ou pas", ce qu'on a fait au début, c'est de remplacer les
Non, pas vraiment, en fait ce qu'on dit, c'est plutôt quequent217 a écrit:En fait je me rend compte que cela revient à poser dans un cas général pour une loi X de densité f,.
Et ça fait que, quand tu divise deux probas de ce type, les
Mais si tu avais un truc du style (j'écrit n'importe quoi)
Modifié en dernier par Ben314 le 08 Aoû 2023, 13:49, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probabilité discrète et continue
Bonjour,
On peut conditionner par une variable aléatoire continue : voir par exemple la page wikipedia https://fr.wikipedia.org/wiki/Esp%C3%A9rance_conditionnelle#Cas_absolument_continu. L'espérance de conditionnée par
conditionnée par  est une nouvelle variable aléatoire, fonction de
est une nouvelle variable aléatoire, fonction de  .
.
On peut conditionner par une variable aléatoire continue : voir par exemple la page wikipedia https://fr.wikipedia.org/wiki/Esp%C3%A9rance_conditionnelle#Cas_absolument_continu. L'espérance de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
